
A Thousand Bells: Acoustical Implementation of Bell Spectra Using the Finite Element Method and Its Compositional Realization (DMA dissertation, deposited in September 2020)
Dissertation Download Link: http://hdl.handle.net/2142/108427
![]()
Listen to the sound of Bell 013, “Overtone Bell”
31 Just-tuned FEM (Finite Element Method) Bell sounds are available now:
Now you can listen to the 31 FEM virtual bell sounds with different harmonic profiles at the bottom of this page.
Presentation on the acoustical models of bell sounds and the modelling of virtual bell shapes and their spectra by synthesizing engineering physics and campanology with music, by using the Finite Element Method (FEM) technique.
A DMA dissertation presentation at the IRCAM Forum Workshops, "Spatialization, Orchestration, Perception, hors les murs"
Montreal (online), February 4–5–6 and 11–12, 2021
Round table : Composing timbre and space, as part of the IRCAM Forum Workshops
Modérateur / Chair—Jonathan Goldman (Université de Montréal)
• Monica L. Bolles, “Orbits: An exploration in spatial audio and sonification”
• Dongryul Lee (University of Illinois at Urbana-Champaign), “A Thousand Carillons: Acoustical Implementation of Bell Spectra Using the Finite Element Method and Its Compositional Realization”
• Anésio Azevedo Costa Neto (Instituto Federal de São Paulo—IFSP / Universidade de Brasília / IDMIL—McGill University), “Cerrado—Applying spatialization techniques to expanded perceptive fields”
• Marlon Schumacher and Núria Giménez-Comas, “Sculpting space”
Montreal (online), February 4–5–6 and 11–12, 2021
![]()
![]()
![]()
![]() Modal vibrations of the four lower modes of the bell: hum [2,0], prime [2,1], tierce [3,1], and quint [3,1#] from Bell 002 (septimal third tierce with just major seventh nominal)
Modal vibrations of the four lower modes of the bell: hum [2,0], prime [2,1], tierce [3,1], and quint [3,1#] from Bell 002 (septimal third tierce with just major seventh nominal)
Three FEM-engineered bell spectra are employed in the first movement, “Motuum Cælestium“ of TIMESTORY, Book I: An Astropastoral for 13 soloists (2020-21).
Check at the following timestamps, 1:20, 3:29, and 5:27.
The main purpose of my dissertation research is to assimilate the harmonic spectra generated by using the Finite Element Method technique into compositional processes. The FEM has been widely used in engineering analysis, especially in the analysis of solids and structures (e.g., dam, bridge, etc.) and of heat transfer and fluids. It been also used in the field of Acoustical Physics, especially for the creation and optimization of carillons. Based on the FEM technique, I create an arbitrary number of virtual bells with physically modelled in virtual space, and their spectral profiles are calculated, and finally, these newly generated harmonic parameters will be adopted and realized in a musical composition with acoustical, notational, and practical expression.
Dissertation Download Link: http://hdl.handle.net/2142/108427
Listen to the sound of Bell 013, “Overtone Bell”
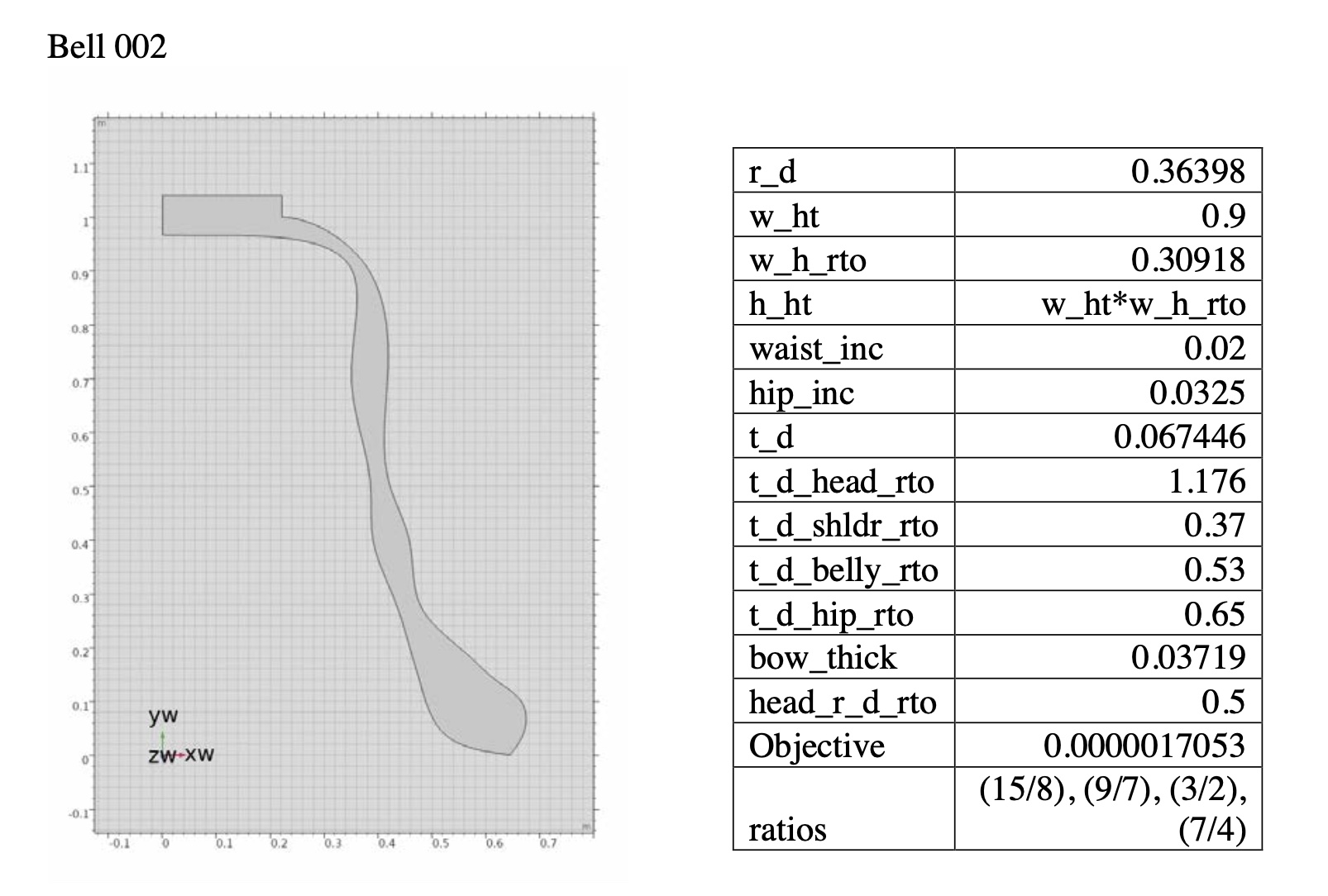
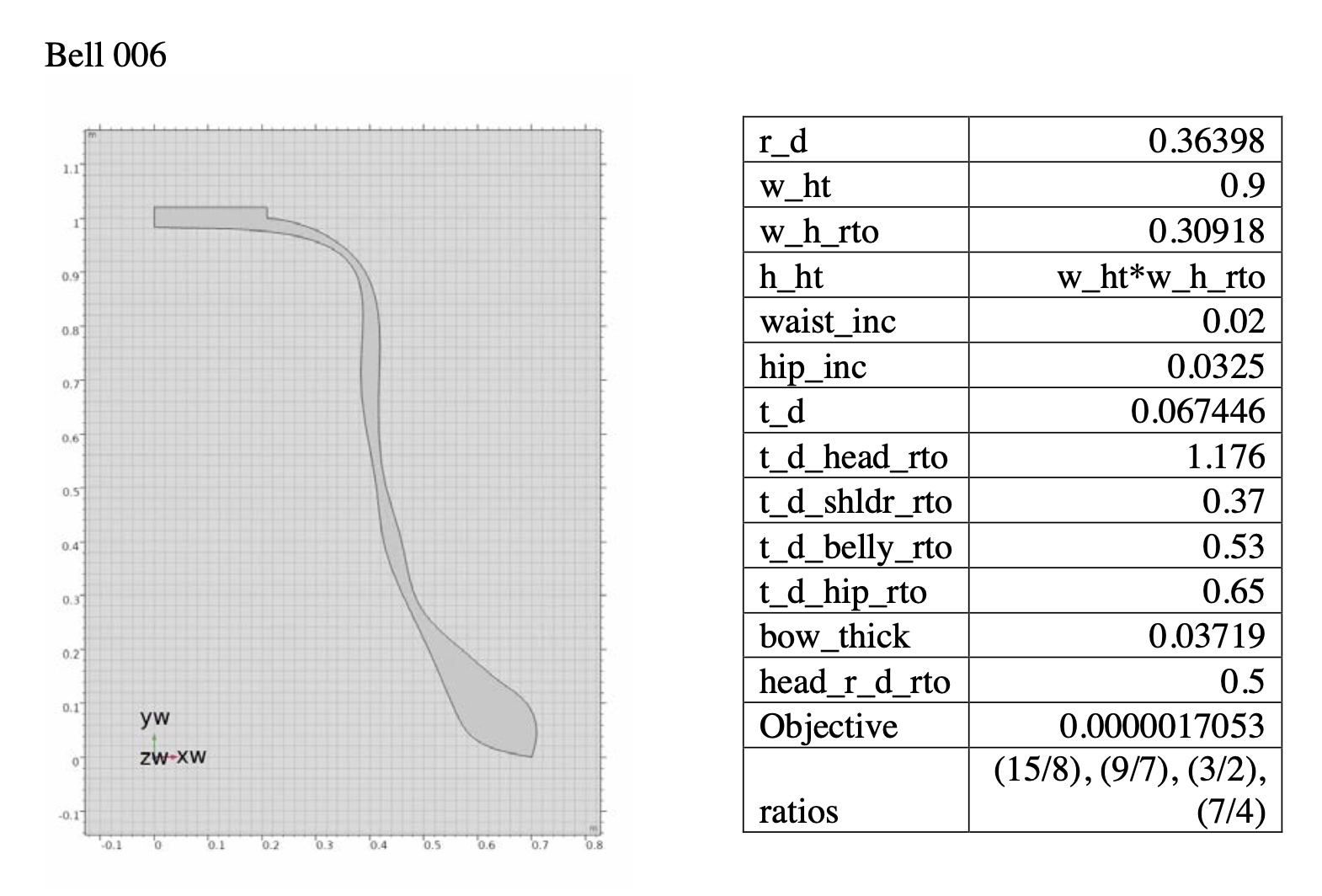
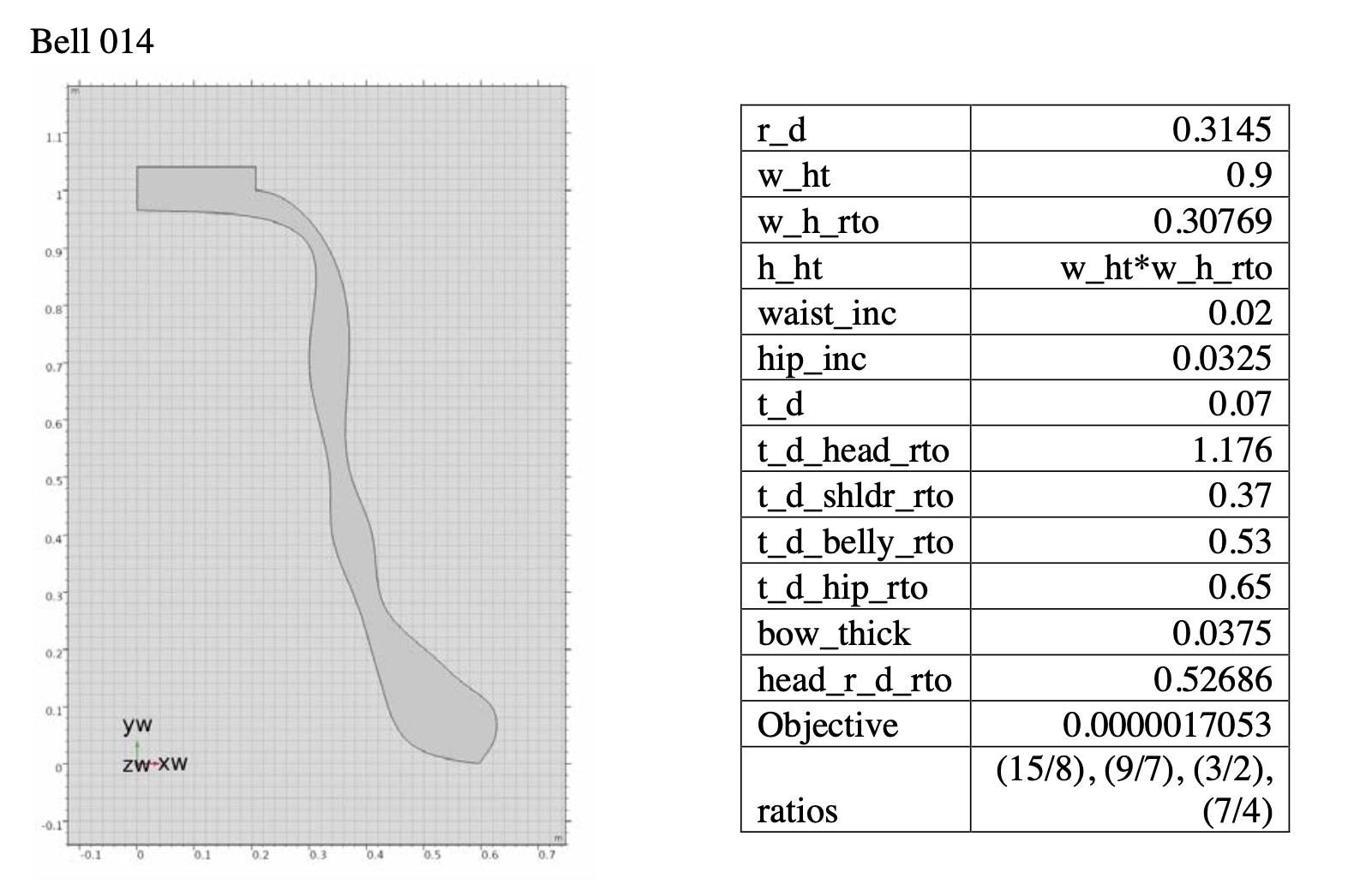
Bell 002–an ideally optimized bell
Prime, Tierce, Quint, Nominal = 15/8, 9/7, 3/2, 7/4
Object function value = 0.0000017053
Prime, Tierce, Quint, Nominal = 15/8, 9/7, 3/2, 7/4
Object function value = 0.0000017053
Bell 023–a non-octave bell with just major 7th prime with “pure” beatings
Prime, Tierce, Quint, Nominal = 16/15, 14/6, 16/11, 15/4
Object function value = 0.0013977
Prime, Tierce, Quint, Nominal = 16/15, 14/6, 16/11, 15/4
Object function value = 0.0013977
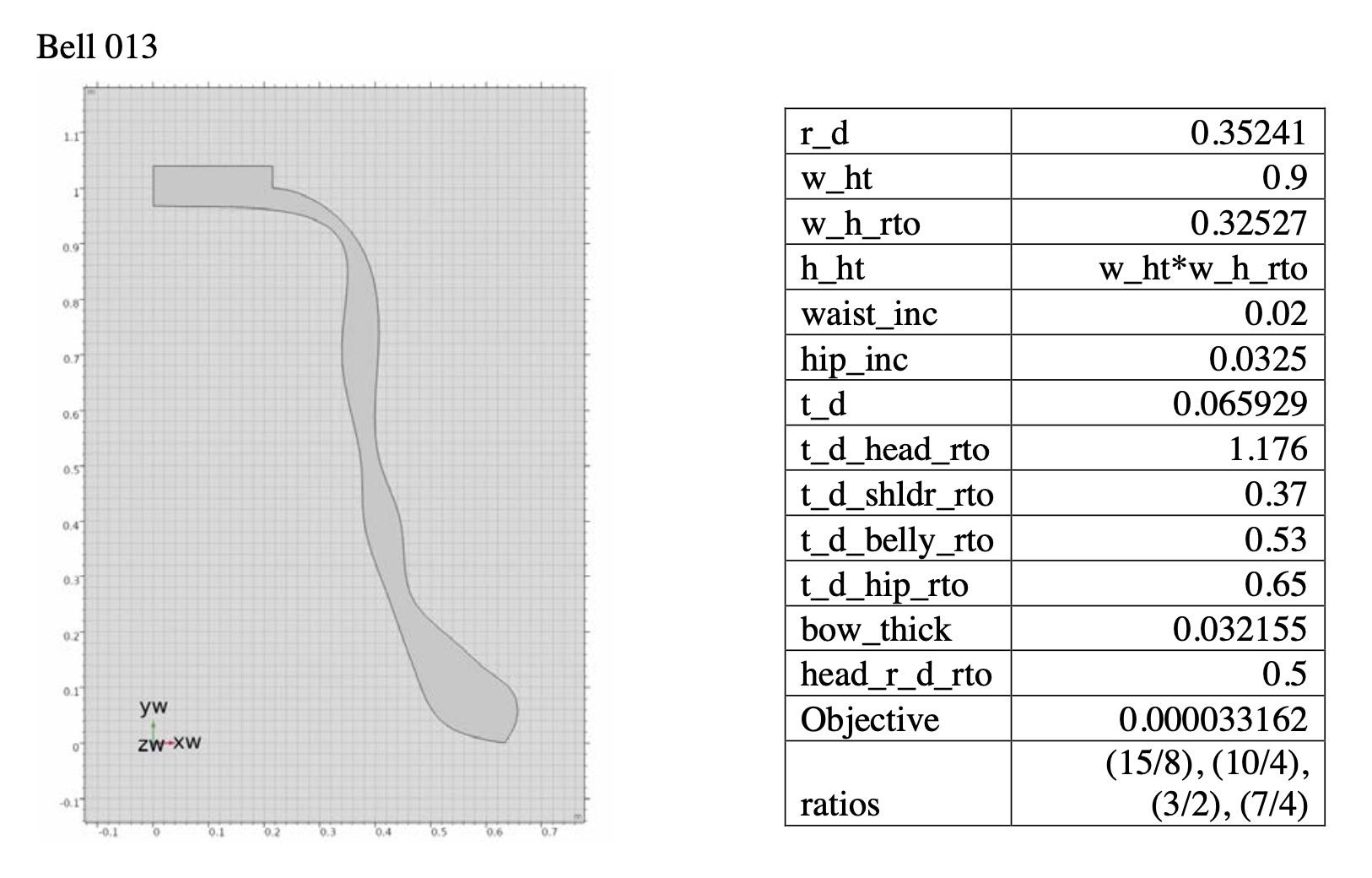
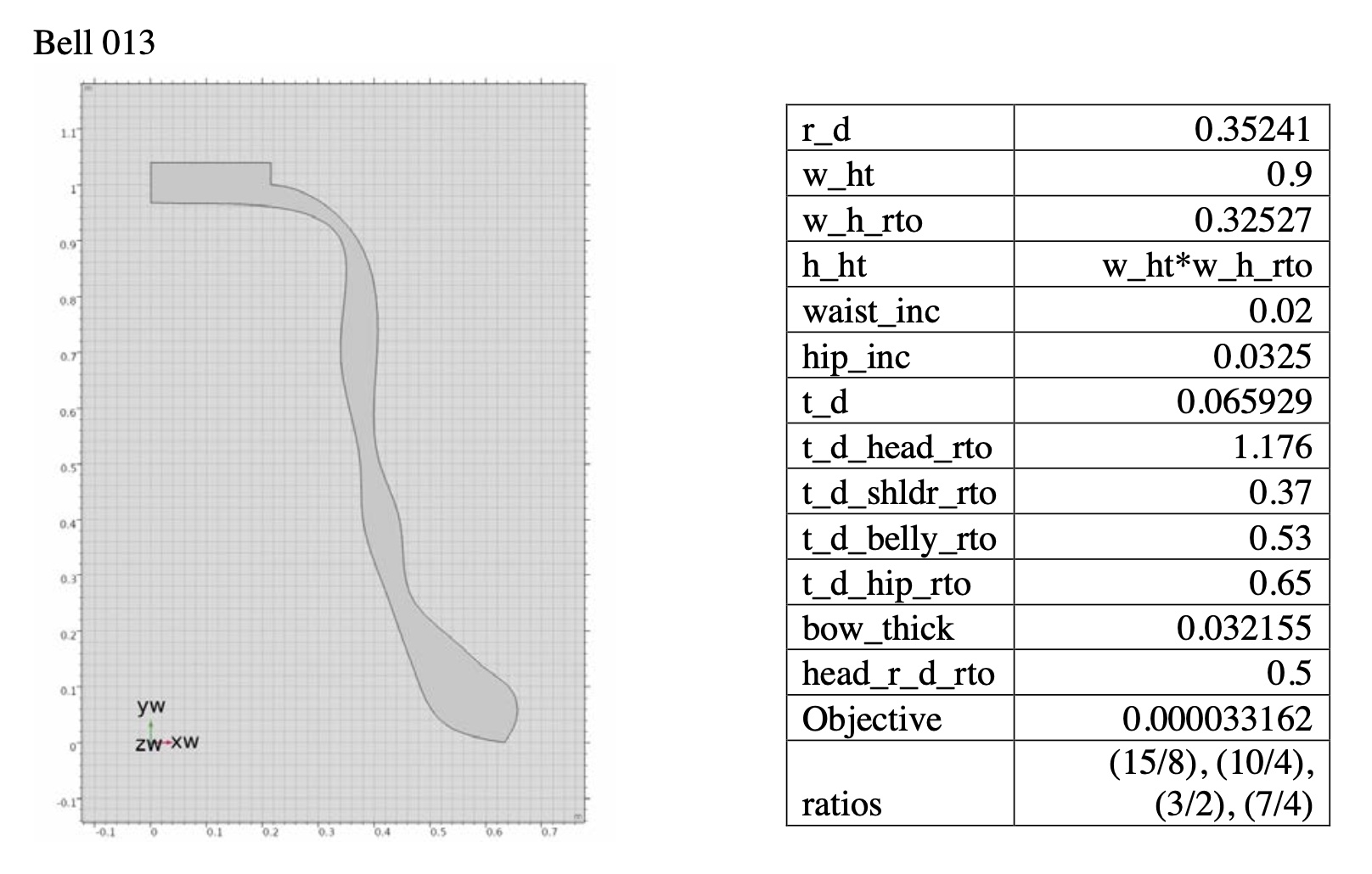
Bell 013–the bell sound material that is used in TIMESTORY, "Overtone Bell"
Prime, Tierce, Quint, Nominal = 15/8, 10/4, 3/2, 7/4
Object function value = 0.000033162
Prime, Tierce, Quint, Nominal = 15/8, 10/4, 3/2, 7/4
Object function value = 0.000033162
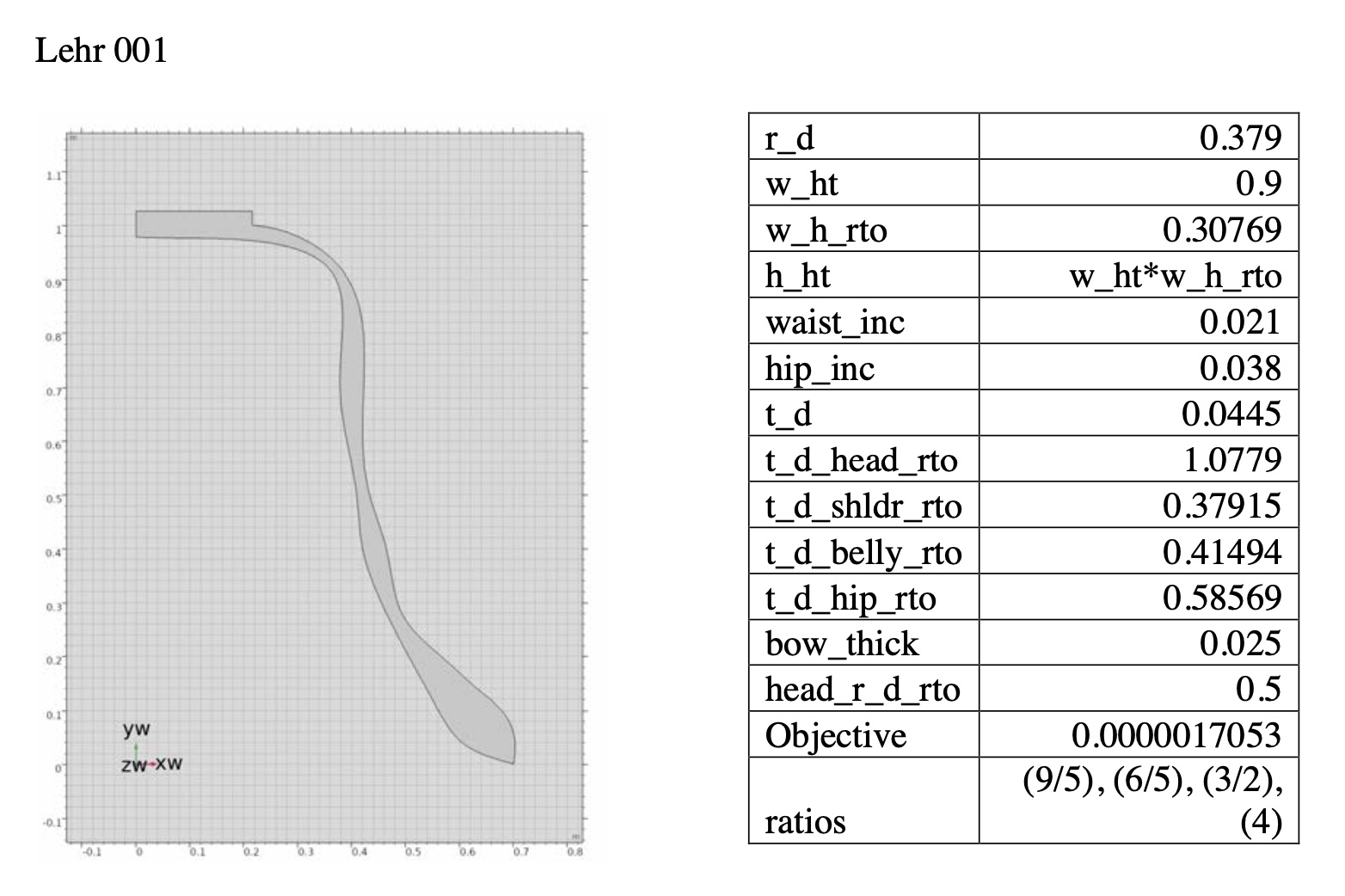
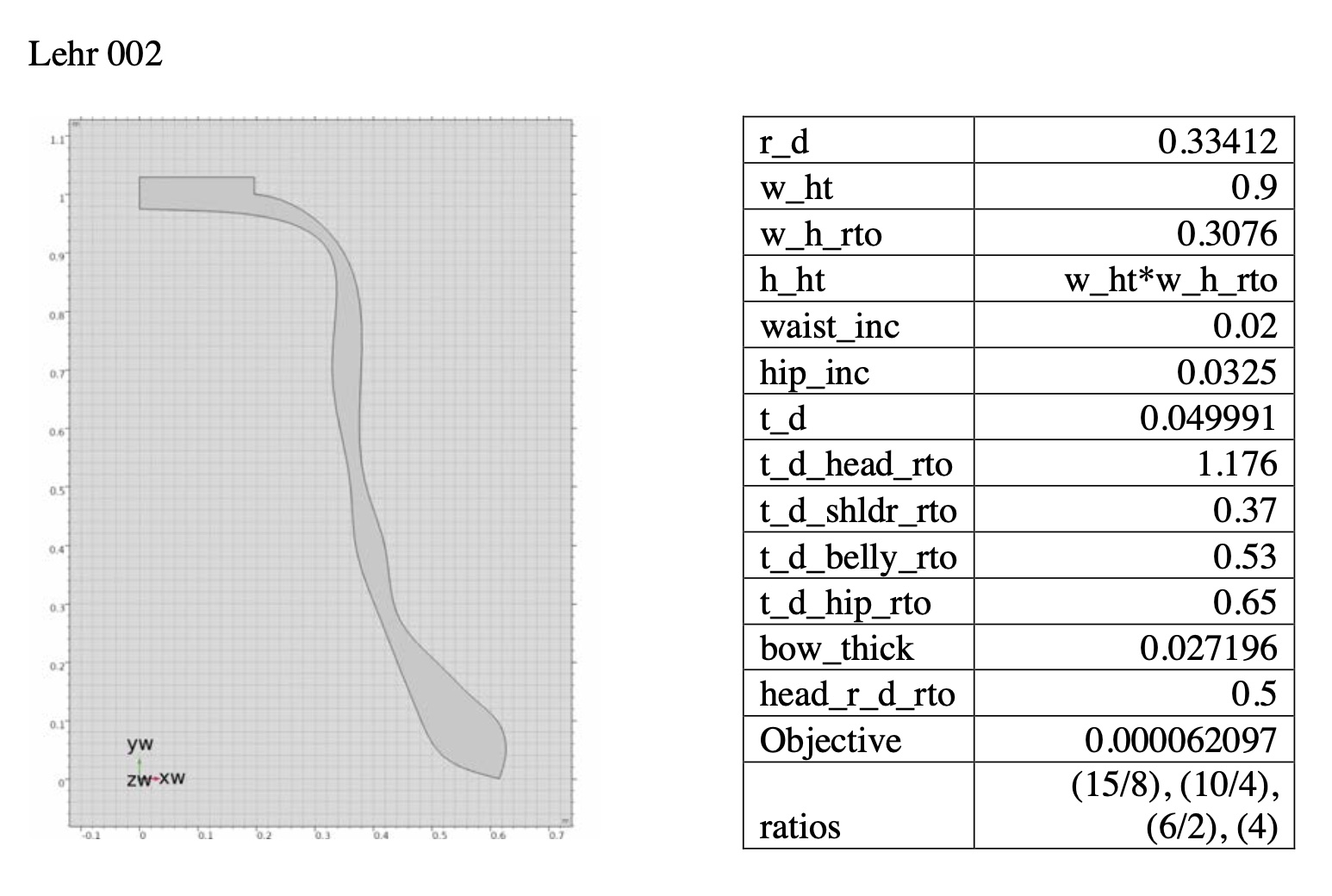
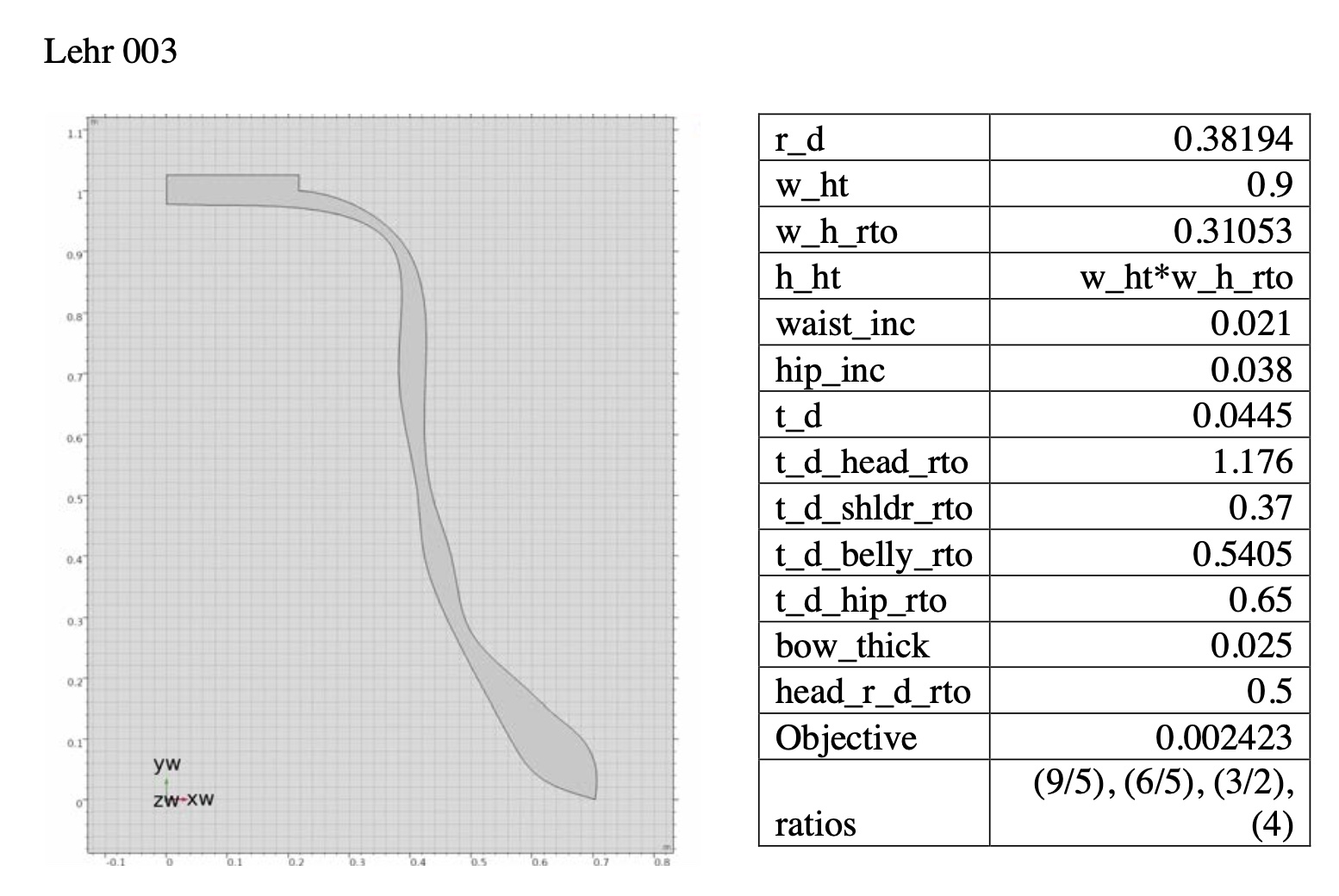
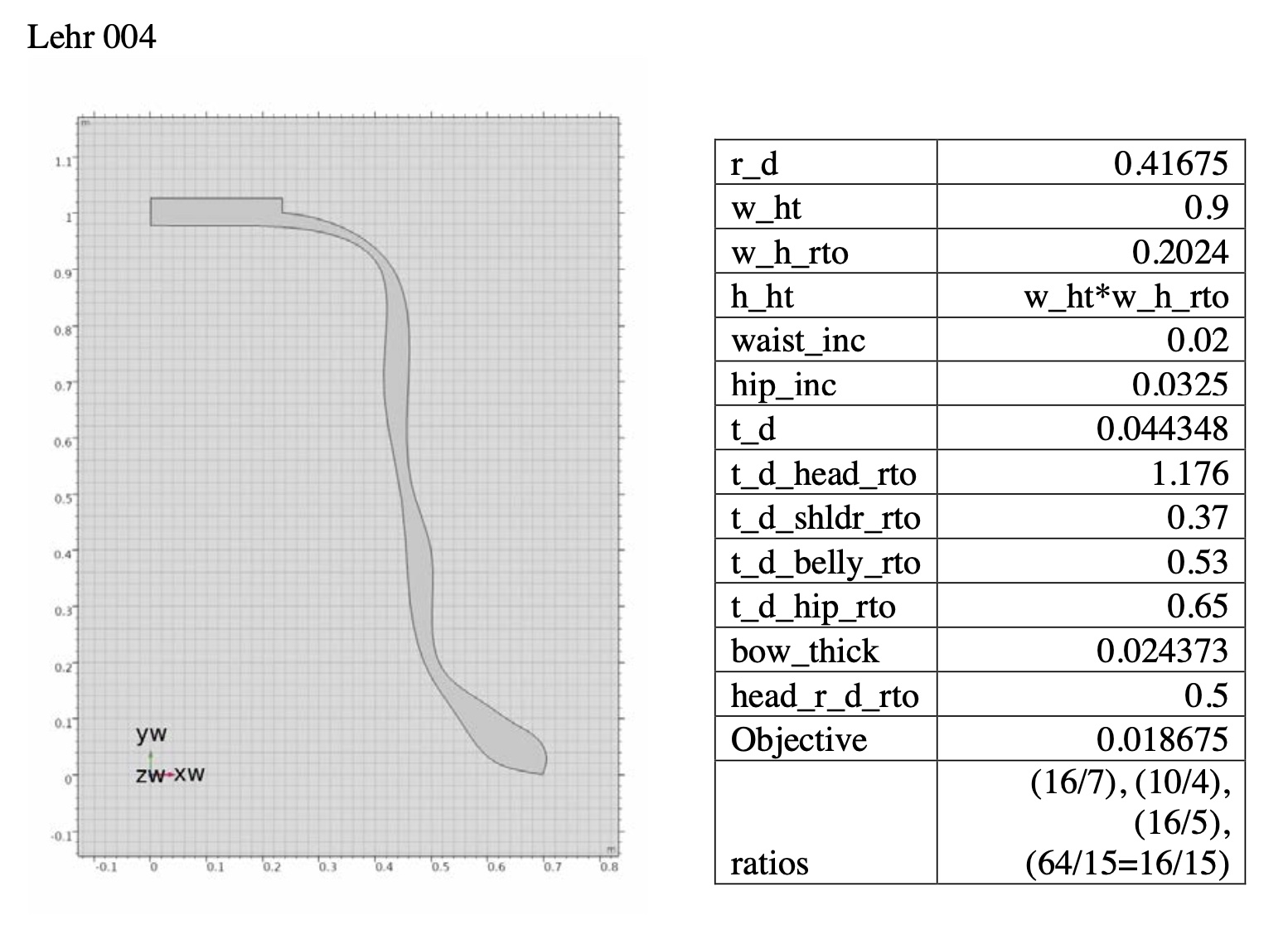
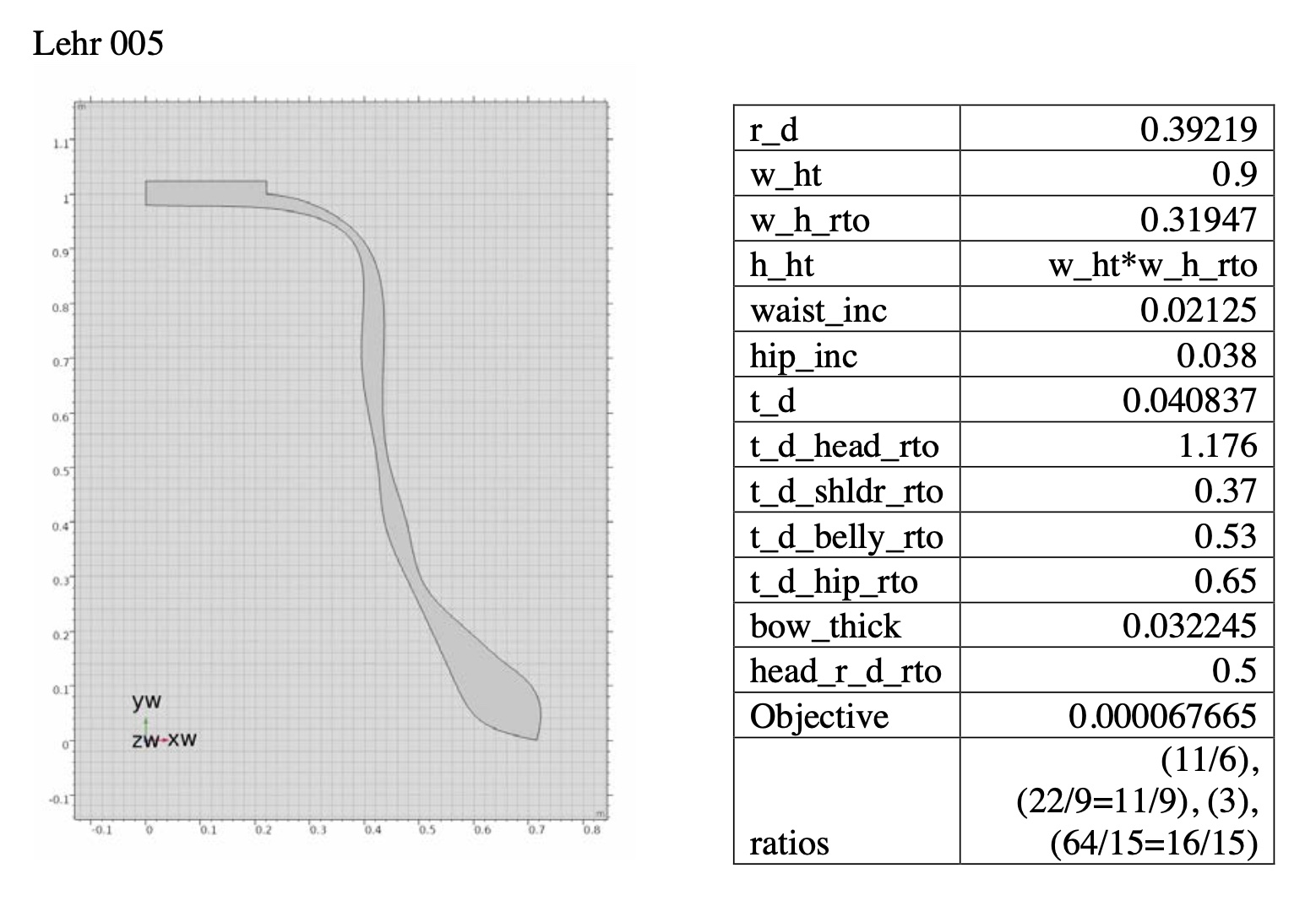
Lehr-Bell 001–a traditional minor-3rd bell from the undertone series
Prime, Tierce, Quint, Nominal = 9/5, 6/5, 3/2, 4
Object function value = 0.000033162
Prime, Tierce, Quint, Nominal = 9/5, 6/5, 3/2, 4
Object function value = 0.000033162
Presentation on the acoustical models of bell sounds and the modelling of virtual bell shapes and their spectra by synthesizing engineering physics and campanology with music, by using the Finite Element Method (FEM) technique.
A DMA dissertation presentation at the IRCAM Forum Workshops, "Spatialization, Orchestration, Perception, hors les murs"
Montreal (online), February 4–5–6 and 11–12, 2021
Round table : Composing timbre and space, as part of the IRCAM Forum Workshops
Modérateur / Chair—Jonathan Goldman (Université de Montréal)
• Monica L. Bolles, “Orbits: An exploration in spatial audio and sonification”
• Dongryul Lee (University of Illinois at Urbana-Champaign), “A Thousand Carillons: Acoustical Implementation of Bell Spectra Using the Finite Element Method and Its Compositional Realization”
• Anésio Azevedo Costa Neto (Instituto Federal de São Paulo—IFSP / Universidade de Brasília / IDMIL—McGill University), “Cerrado—Applying spatialization techniques to expanded perceptive fields”
• Marlon Schumacher and Núria Giménez-Comas, “Sculpting space”
Montreal (online), February 4–5–6 and 11–12, 2021

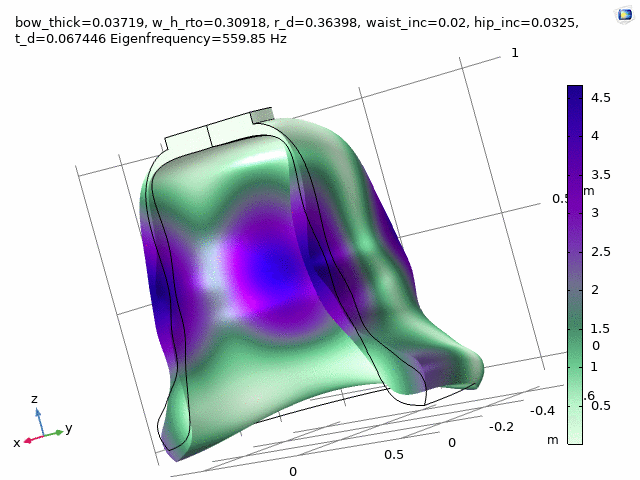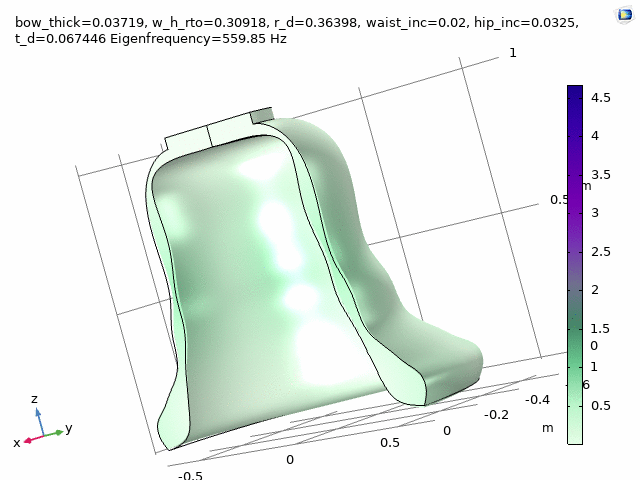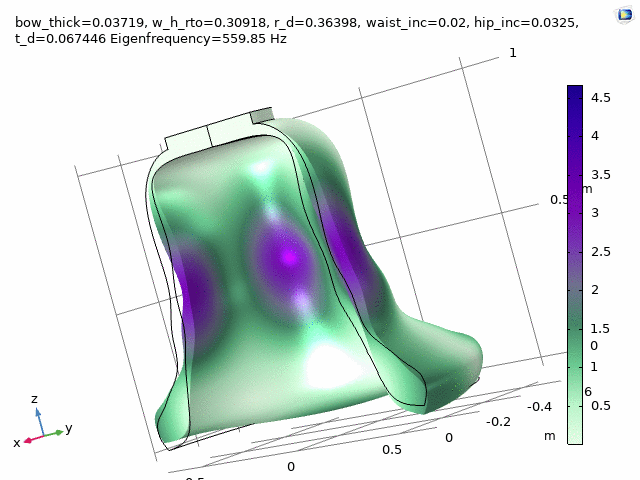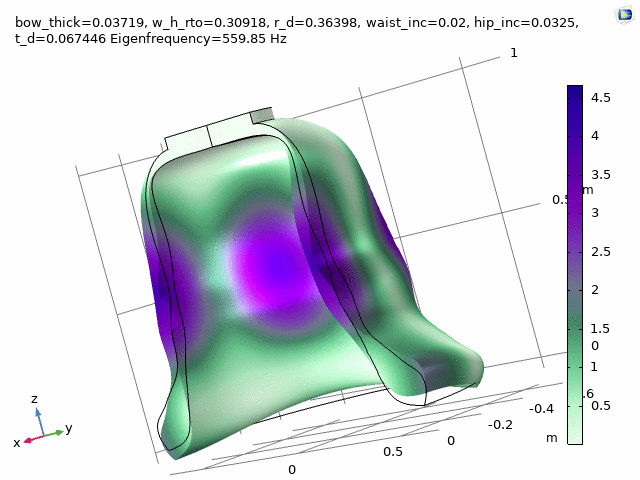
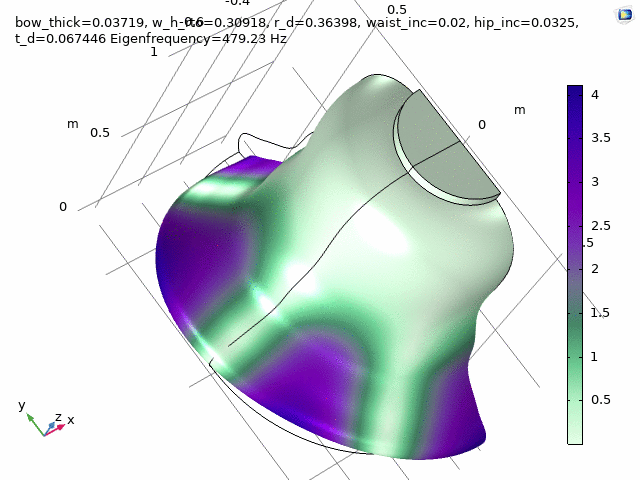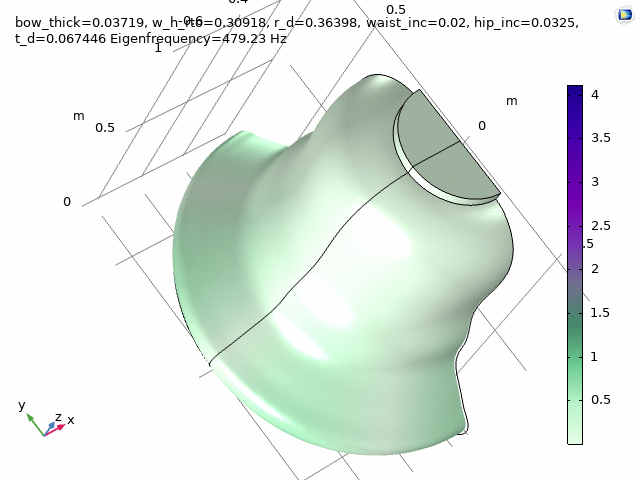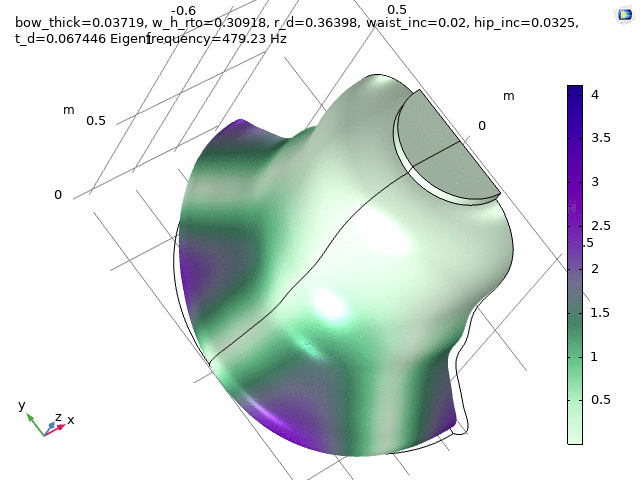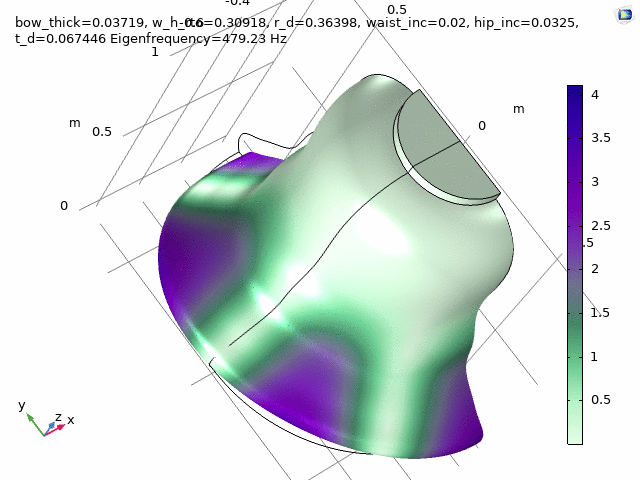
Three FEM-engineered bell spectra are employed in the first movement, “Motuum Cælestium“ of TIMESTORY, Book I: An Astropastoral for 13 soloists (2020-21).
Check at the following timestamps, 1:20, 3:29, and 5:27.
The main purpose of my dissertation research is to assimilate the harmonic spectra generated by using the Finite Element Method technique into compositional processes. The FEM has been widely used in engineering analysis, especially in the analysis of solids and structures (e.g., dam, bridge, etc.) and of heat transfer and fluids. It been also used in the field of Acoustical Physics, especially for the creation and optimization of carillons. Based on the FEM technique, I create an arbitrary number of virtual bells with physically modelled in virtual space, and their spectral profiles are calculated, and finally, these newly generated harmonic parameters will be adopted and realized in a musical composition with acoustical, notational, and practical expression.

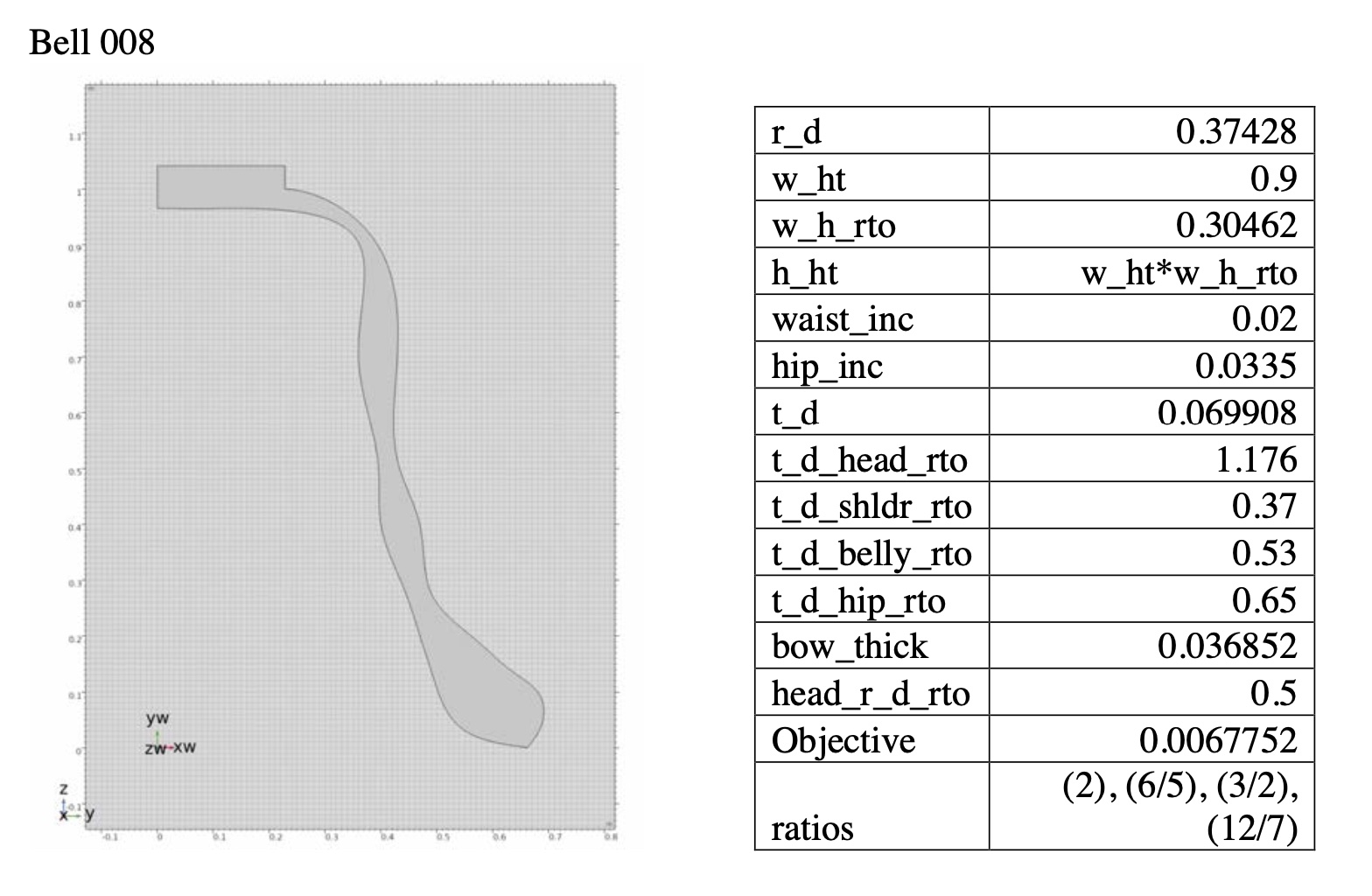
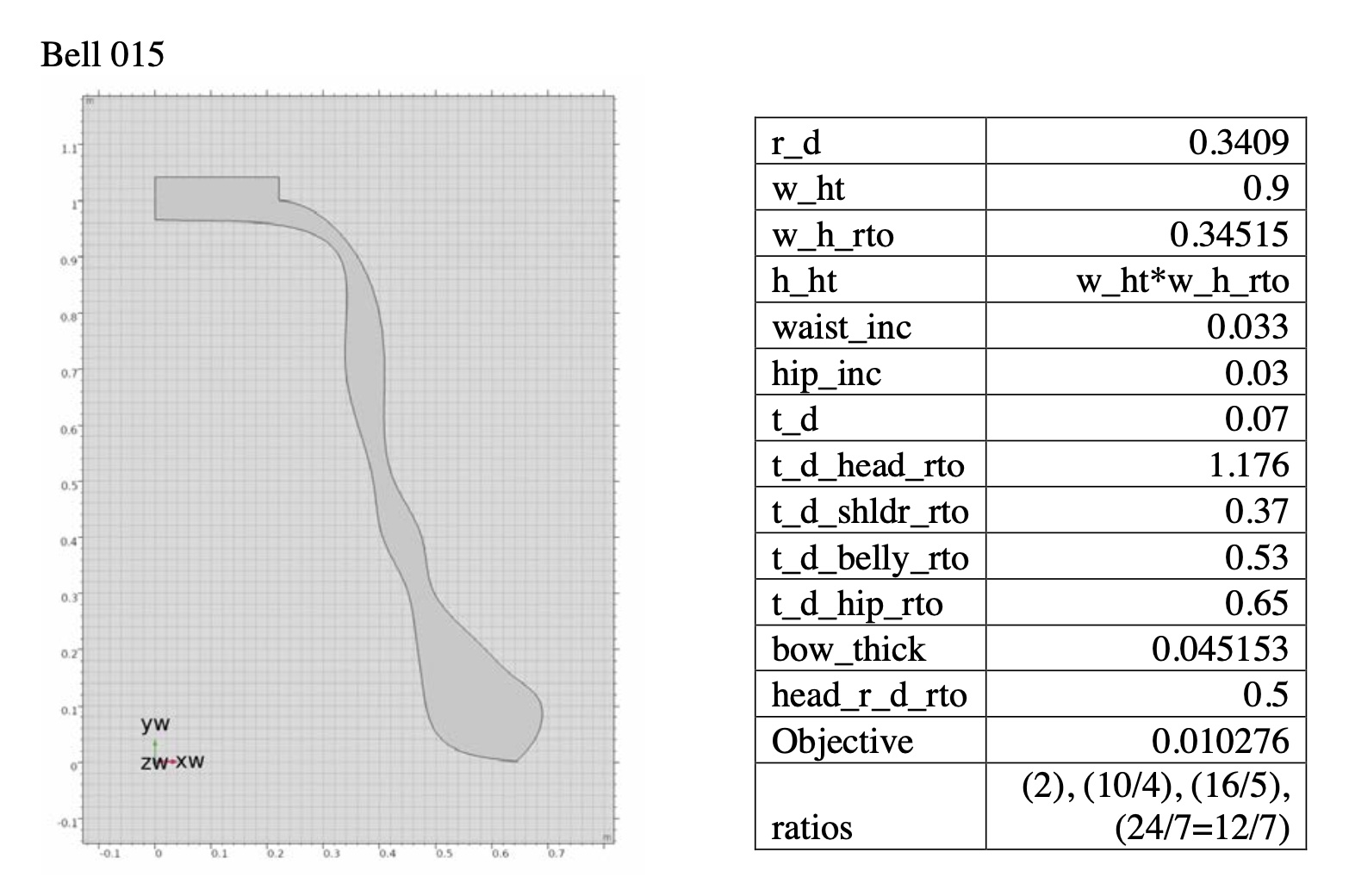
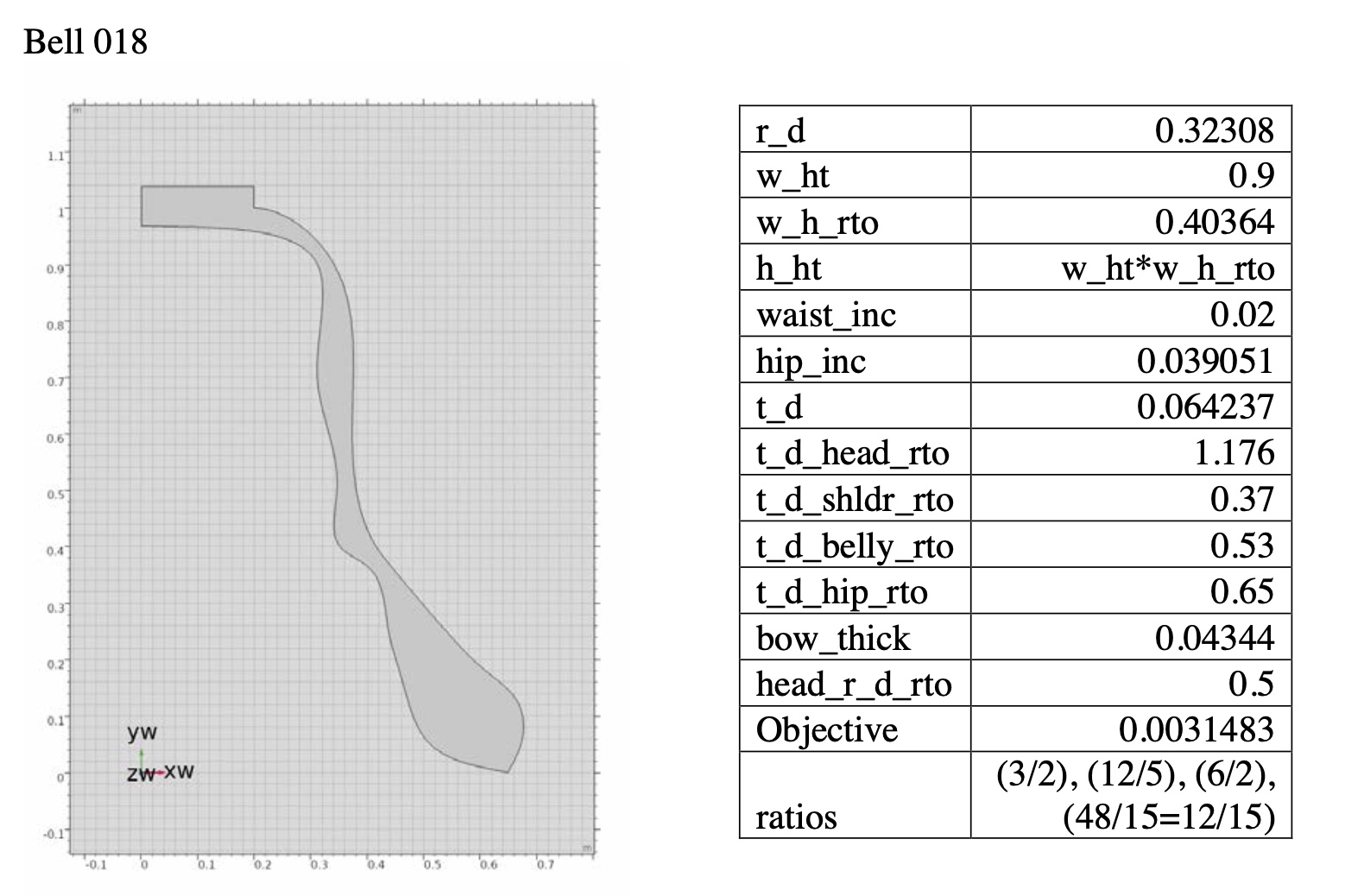
2D Geometry of Bell 018 (just minor third tierce with just minor ninth nominal bell)
The first chapter provides a brief introduction of pre and post-spectral music that is inspired by or employs bell sounds from which it derives its central materials. This includes music by Toshirō Mayuzumi, Jonatha Harvey, Tristan Murail, Magnus Lindberg, and works by the author.
The second chapter introduces bell acoustics and the creation of new spectral profiles of optimal bell tone colors based upon just tuning ratios. In this chapter, I discuss how the concepts of consonance and Just Noticeable Difference in psychoacoustics are applied to use the 96 tone equal temperament tuning system for bell harmonic profiles.
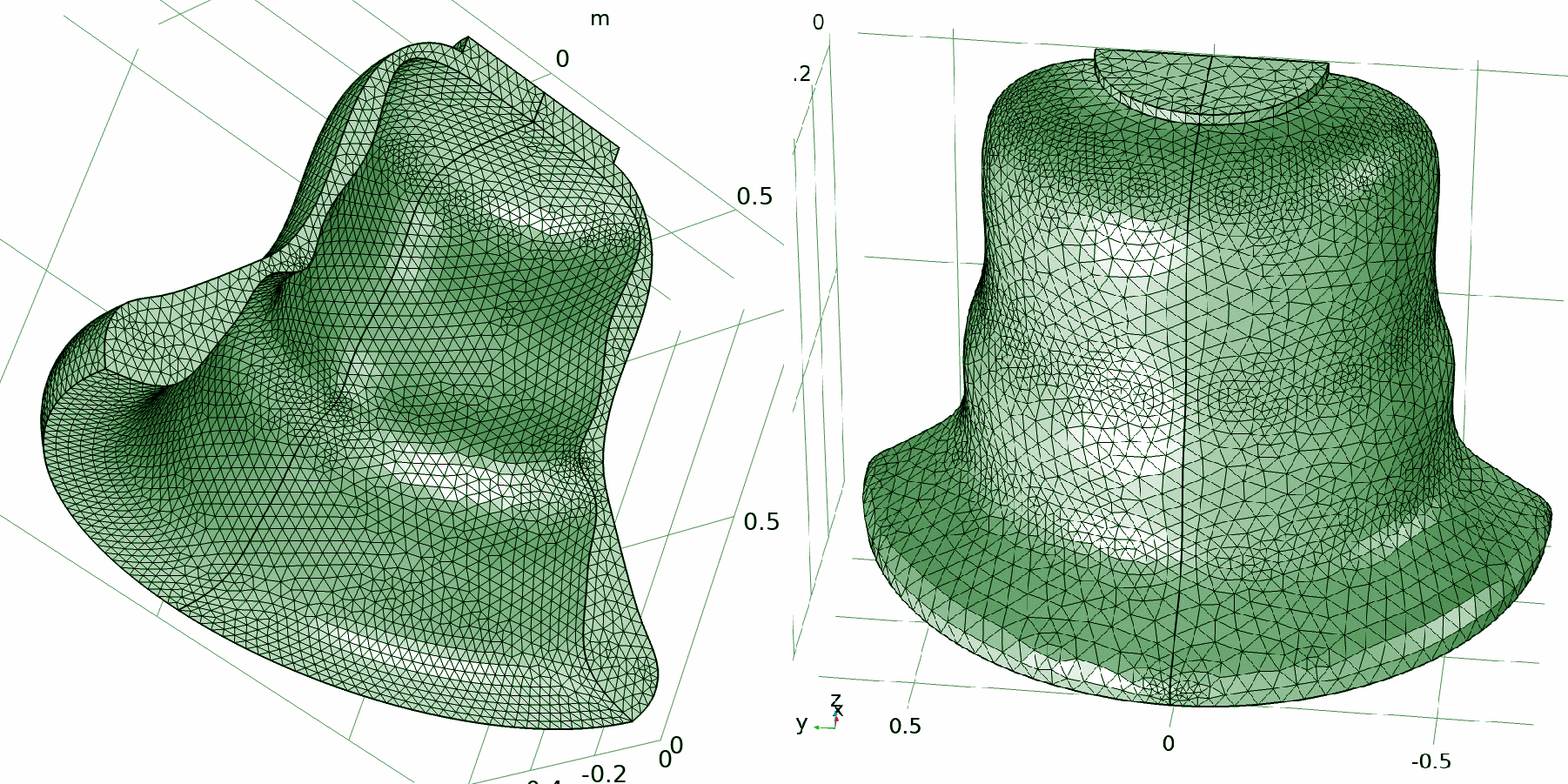

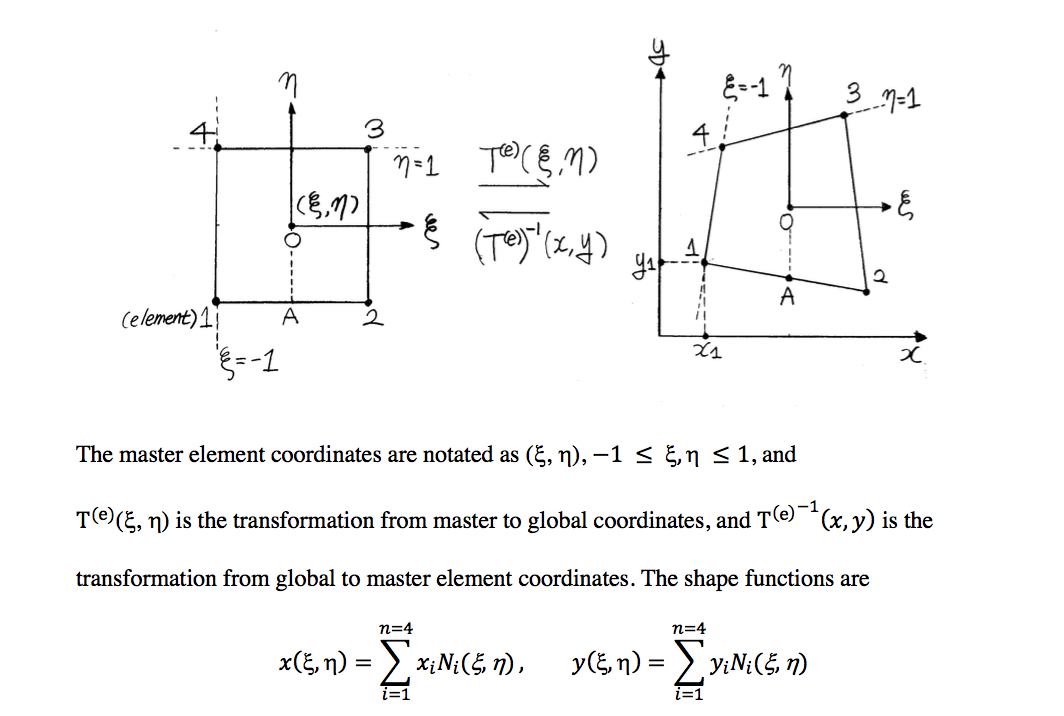
The third chapter includes the theoretical basis of the FEM and its application to the isoparametric 2-D quadrilateral elements, which are the fundamental theories of how bell harmonies are mathematically calculated. This includes the central concepts of the FEM, such as the Principle of Virtual Work/Displacement, master to global coordinate transformation, FE shape functions, usages of Jacobian matrices, numerical integration of the stiffness matrix and the equivalent nodal force vector for the element by using the Gauss-Lagrange quadrature.

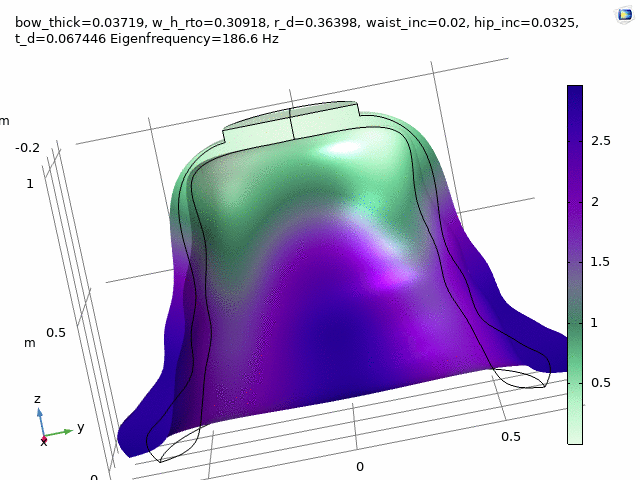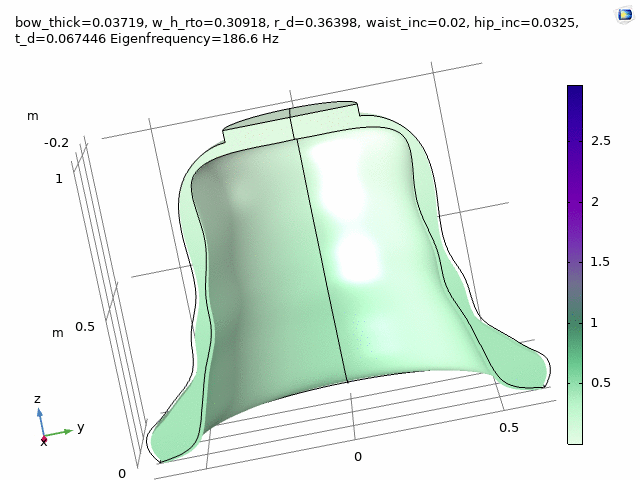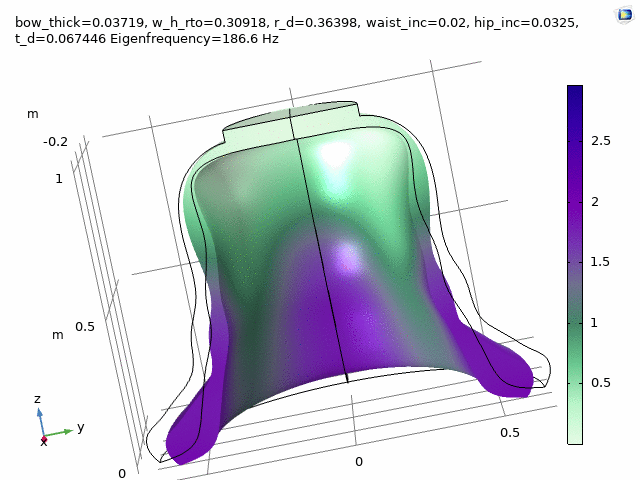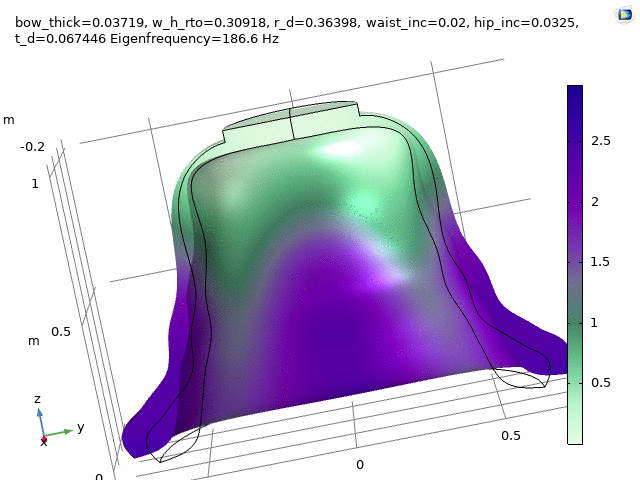
Nodal circles and nodal meridians /displacement fields of lower four modes: prime [2,1], tierce [3,1], quint [3,1#], and nominal mode [4,1]
In the fourth chapter, I create bell model geometry by
using 2D bell nominal curve and adjustable design variables. Physical
parameters, such as the Poisson ratio, Young’s modulus, and material properties
are also adopted from previous bell design research. Based
upon the aforementioned prototypes, I create 24 different 3-D bell geometries,
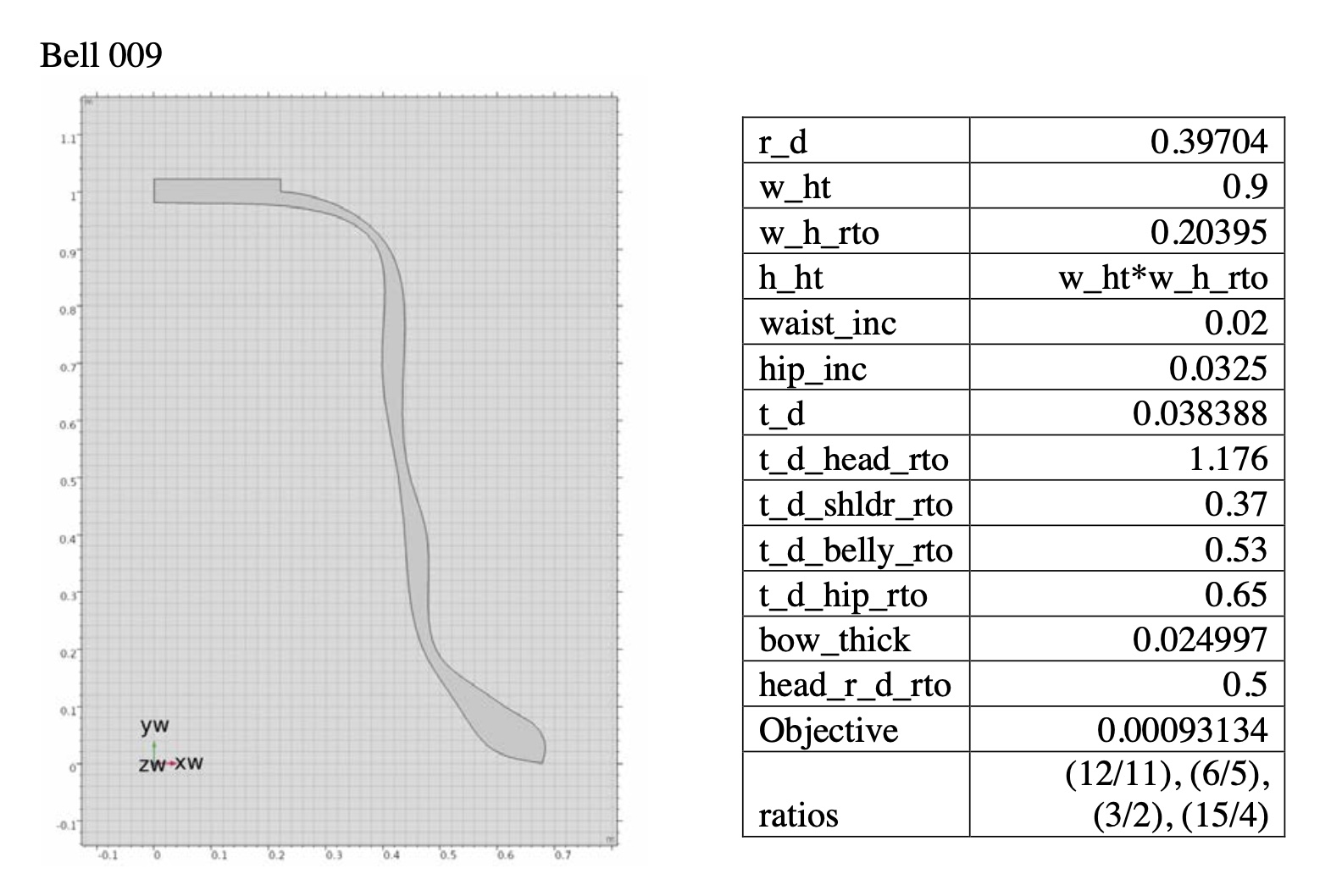
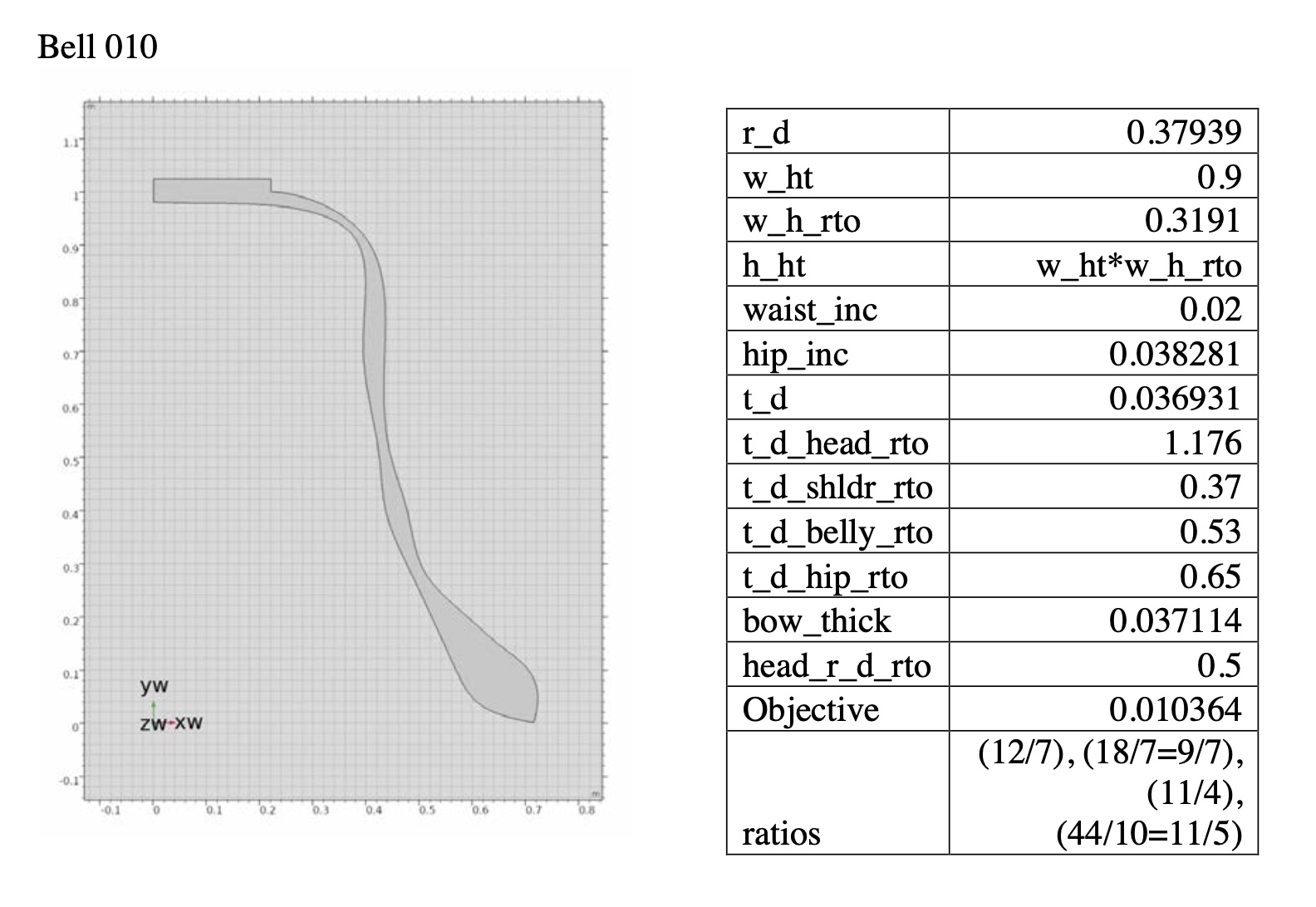
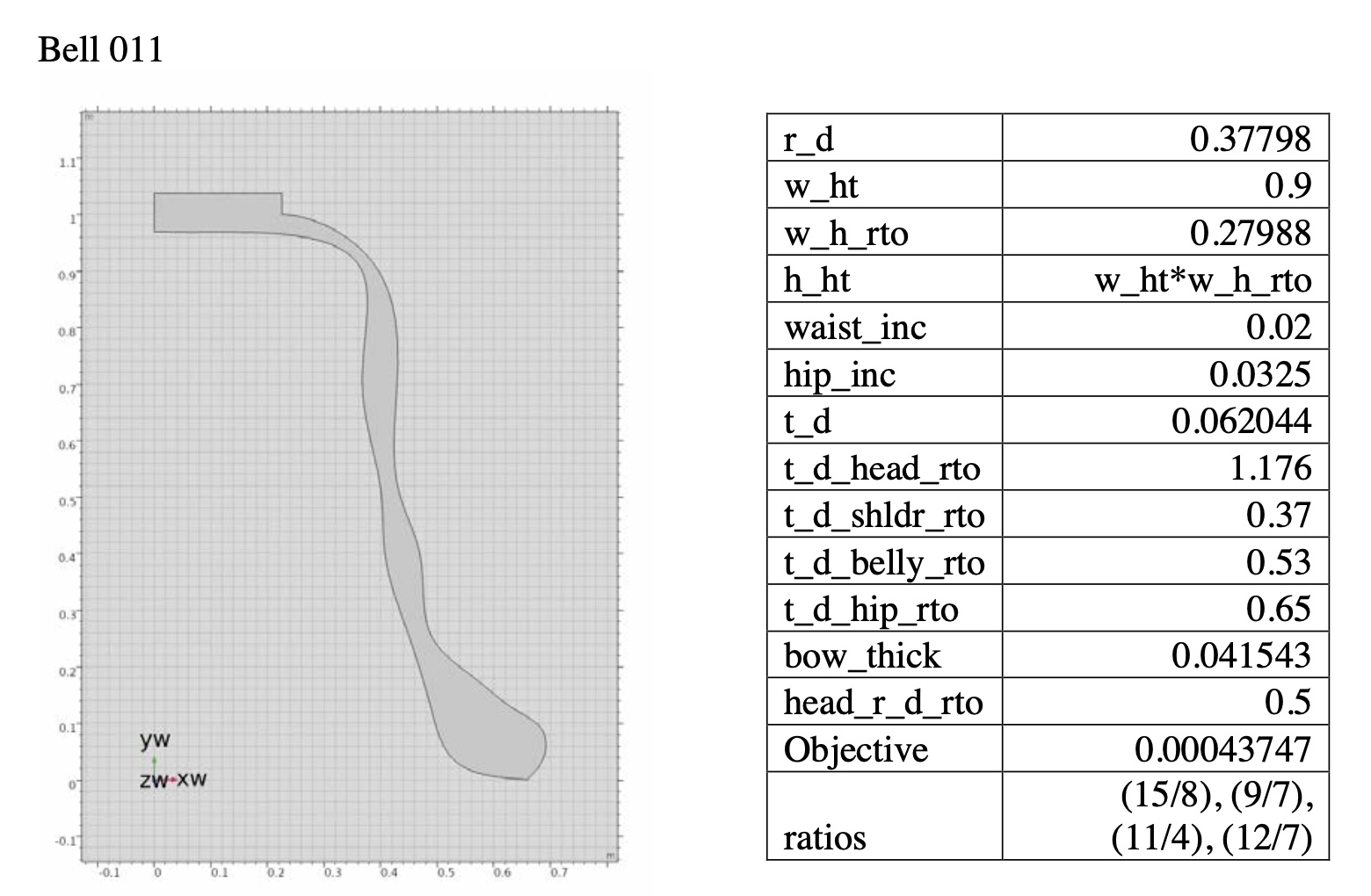
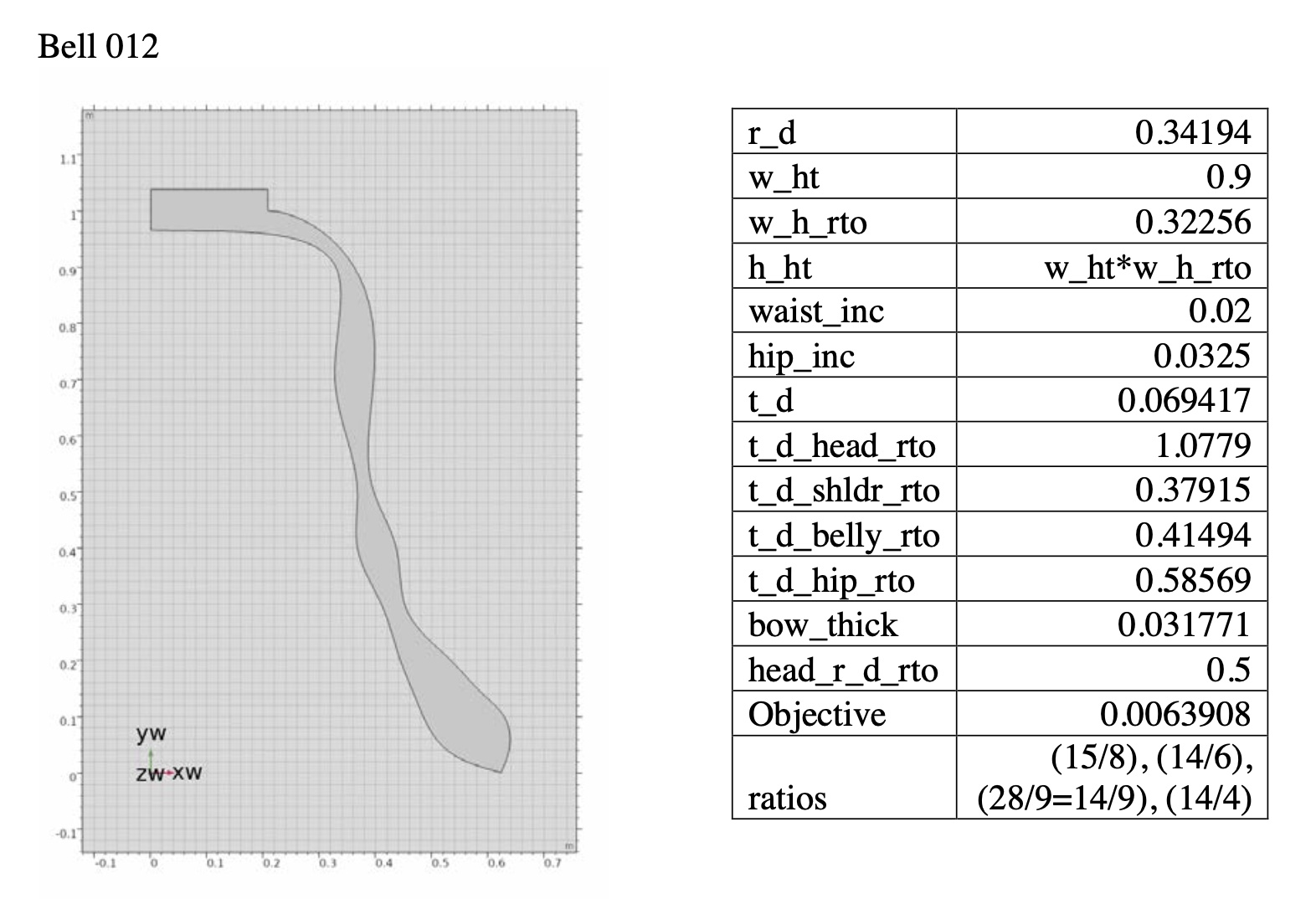
and analyze the spectra of these virtual bells. These bell models are analyzed,
optimized and tuned to create tone colors that are defined in Chapter 2. After
a validating process of the bell model, the general backgrounds of optimization theory are also introduced and analyzed
for the purpose of creating 3-D virtual bells.

Parametric sweep graph of frequency tracking, by adjusting waist:hip ratio parameter
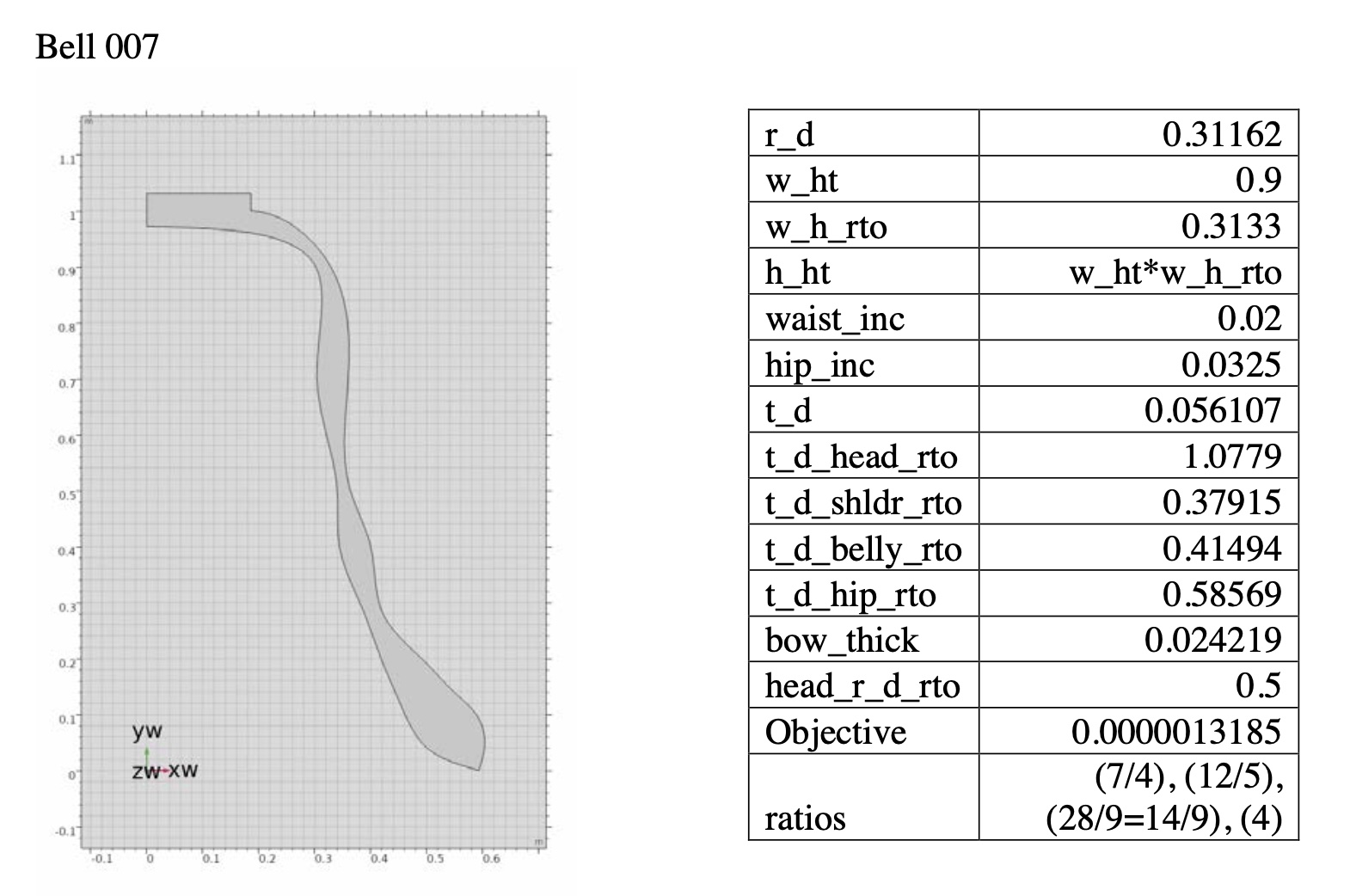
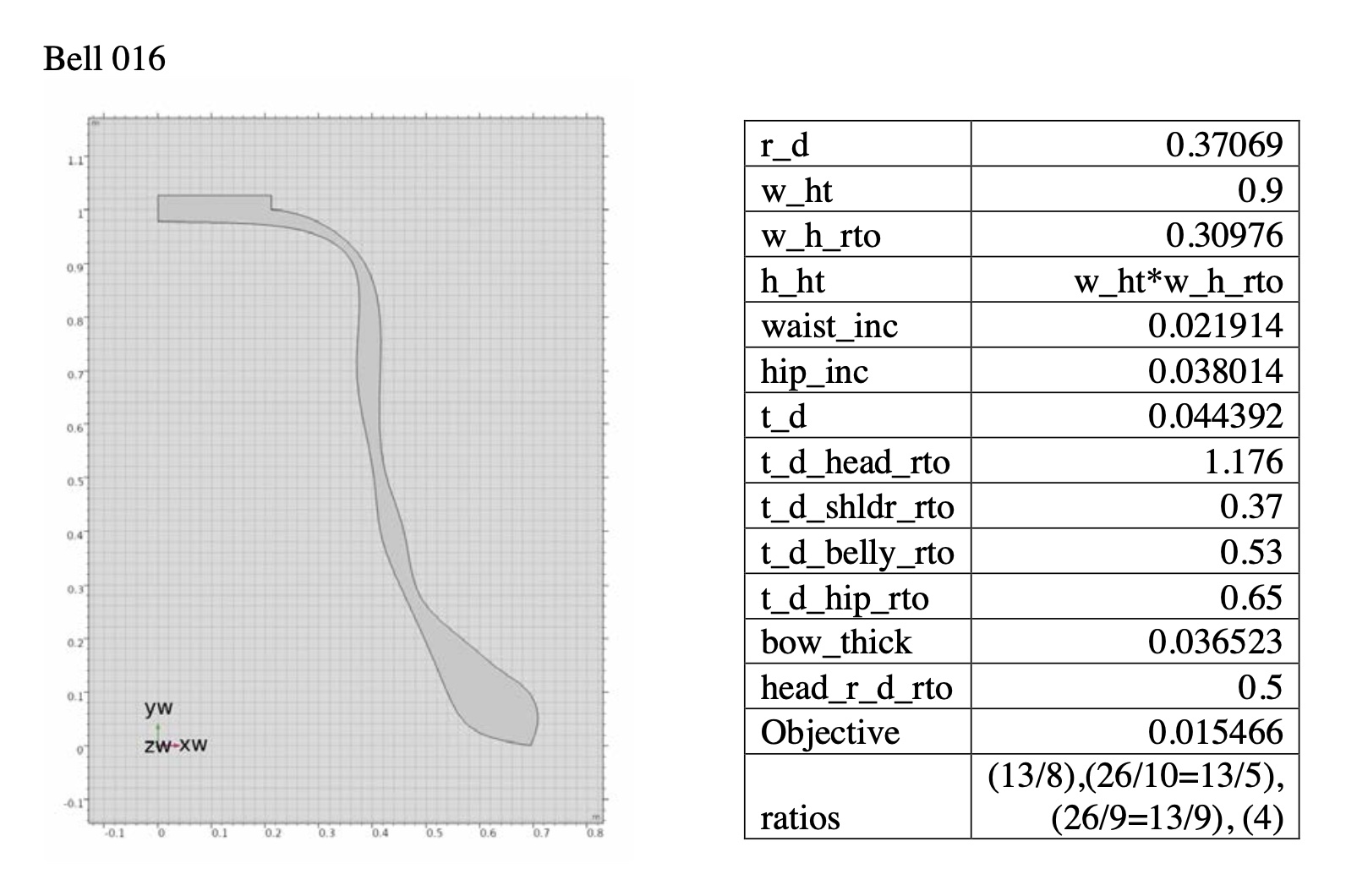
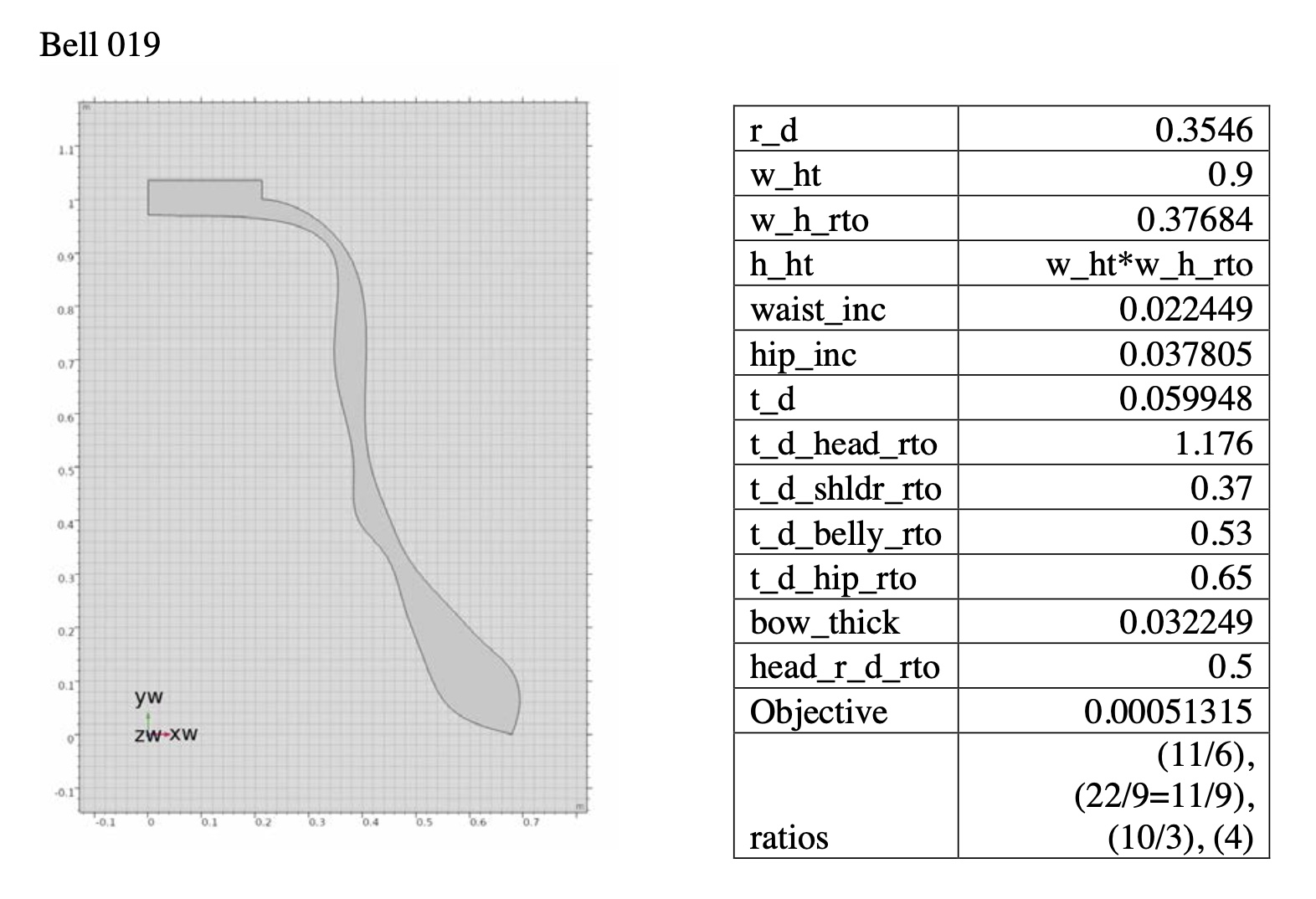
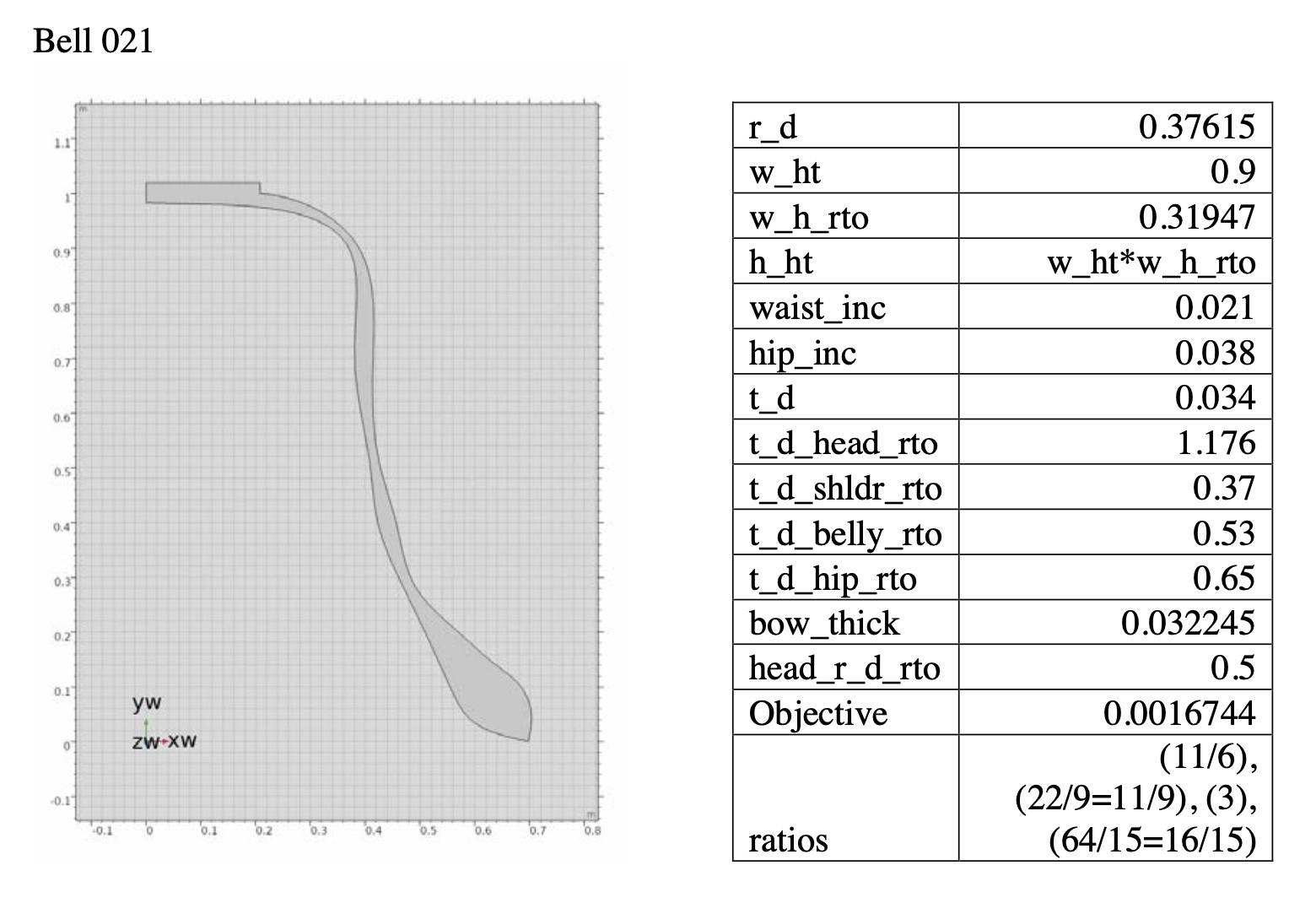
By using the gradual transfigurations of virtual bells, in this dissertation I want to present an original musical “passing spectra” by using the physical modeling and its resultant acoustical data. In this example, the beginning harmony is from Bell 018 (perfect fifth prime with just minor 3rd tierce and just minor 9th nominal), and the final arrival harmony is from Bell 013 (just major third tierce with just major seventh prime and harmonic minor seventh nominal).

Transfiguration of bell geometry from Bell 018 to Bell 013.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
My future pieces, including the new work for Grossman ensemble, which is commissioned by the Chicago Center for Contemporary Composition, will use a substantial amount of musical material based on generated bell harmonies from the research. This
newly generated timbre-harmonic system will be realized by specially
tuned acoustic instruments and a microtonal synthesizer, which I had
previously engineered and programmed. As such, I intend to further the
theory of harmony established by earlier spectral composers, and develop
analytical research, focused primarily on the analysis of mathematical
and acoustical models of campanology.
Bell Sounds
![]()
![]()
Bell Sounds












The beautiful McFarland Carillon I administered for 3 years (2015–2017) located on the south quad at the University of Illinois. It is 185-feet tall and made up with 49 dutch bells ranging from low C3 to high C7.
The combined weight of the bells is about 15.5 tonnes and their combined cost is half-a-million dollars. The carillon is controlled by MIDI and a MIDI receptor/controller (named “Singing Tower”) located in the tower.
![]()
![]()
![]() The McFarland Carillon and bird figures, painted by Aaron Scythe on the wheel-thrown and bisque fired cylindrical tea bowl, commissioned by the author.
The McFarland Carillon and bird figures, painted by Aaron Scythe on the wheel-thrown and bisque fired cylindrical tea bowl, commissioned by the author.
GOETHE’S GARDEN (2016-17)
On Goethe's Garden, "Structural Foundation of Musical Materials in my Goethe’s Garden: The graphical representation of infinitely recursive fractal tree figures and It’s projection onto the sonic pane"
36 min. video lecture on the algorithmic process of controlling time and frequencies by using Chaotic Dynamical System in my composition, Goethe’s Garden for two pianos tuned a quarter-tone apart (May 2021)
ON A WINTER’S NIGHT A TRAVELLER, THE DEEPLY LEARNED CLAVIER (2022-23)
![]()
On a Winter’s Night a Traveller, The Deeply Learned Clavier (2022–23), work-in-progress
for Solo Piano
피아노를 위한, “겨울 밤의 여행자에 대하여"
Duration: ca. 25 minutes
Program notes
As you can see here on my website, I recently replaced many images on my homepage with artificially synthesized images created by a Deep Learning application. Almost about a half of images that you see here are generated by the “discord.” The speed of development of AI and Deep Learning algorithms are truly remarkable, and the artists of the 21st century may have to compete with AI machines. Rather than compete with the technology, I decided to accept machines as my creative partners.
In 2022, I embarked on a new chapter of my research on Computer Music, in the field of Artificial Intelligence and Deep Learning. I began attending the MIT OCW’s Deep Learning course, as I did in 2010 to study differential equations which significantly contributed to my DMA research. For this, I began studying and analyzing Python and Keras programming languages and codes on the Google Colab platform to implement my own Deep Learning model. For about two months, I played with the code and could make the computer learn about 110 piano pieces written by Mozart. Then, after between one and six hours of each learning process (ca. 20-200 epochs in deep learning), the computer wrote a new piano work within its understanding of the music of Mozart. In other words, the computer wrote a pastiche piece in the style of Mozart, or even tried to counterfeit the works by Mozart.
![]()
Deep Learning generated Output 020, sequence size 25, temperature 2, 74 epochs of learning
![]()
Deep Learning generated Output 062-2, 109 learned works, sequence size 256, weight: 0.085, learning rate: 0.001, optimization: RMSProp, 200 epochs of learning, temperature 3.7
![]()
Deep Learning generated Output 063-6, 109 learned works, sequence size 256, weight: 0.085, learning rate: 0.001, optimization: RMSProp, 30 epochs of learning, temperature 3.9, seed piece: Fantasy in c minor KV366
![]()
Original handwritten score of On a Winter’s Night a Traveller, The Deeply Learned Clavier
Because of the limit of my access to the Google Colab platform, I couldn’t spend enough time on the deep-learning process of more than six hours for each output, and also the number of model data-works was not enough to generate a real Mozart-like piano work, e.g., having an Alberti bassline or crisp and concise phrase models which we can easily find in his oeuvre. However, those outputs/works generated by the computer implied various interesting features that we can often find in the tonal music repertoires, including ambiguous tonalities (in-between different keys), diatonic scales, repetitions, chords and arpeggios, oftentimes realized in awkward, crude and rudimentary, anti-contrapuntal and artificial, or even distorted and mechanic ways.
For about a month I listened to the outputs generated by the computer, and began tracing the trajectories of the computer’s thoughts. I was almost an archeologist who discovered a pile of unfinished, improvisatory, spurious sketches written by an unknown composer or had been misattributed to Mozart(‘s virtual clumsy pupil, if more accurately described.) During the discovery process, I tried to reveal the computer’s intentions, develop his/her imagination, and transformed it into my own artwork.
This project is currently a work-in-progress. Although I tried to complete it by January 2023, because of my other workload, I hope to finish the piece by the Spring or Summer of 2023. It is commissioned by the Boston-based pianist Ariel Mo, who beautifully world-premiered my Le Tombeau de Harvey in January 2022.

On Goethe's Garden, "Structural Foundation of Musical Materials in my Goethe’s Garden: The graphical representation of infinitely recursive fractal tree figures and It’s projection onto the sonic pane"
36 min. video lecture on the algorithmic process of controlling time and frequencies by using Chaotic Dynamical System in my composition, Goethe’s Garden for two pianos tuned a quarter-tone apart (May 2021)

for Solo Piano
피아노를 위한, “겨울 밤의 여행자에 대하여"
Program notes
As you can see here on my website, I recently replaced many images on my homepage with artificially synthesized images created by a Deep Learning application. Almost about a half of images that you see here are generated by the “discord.” The speed of development of AI and Deep Learning algorithms are truly remarkable, and the artists of the 21st century may have to compete with AI machines. Rather than compete with the technology, I decided to accept machines as my creative partners.
In 2022, I embarked on a new chapter of my research on Computer Music, in the field of Artificial Intelligence and Deep Learning. I began attending the MIT OCW’s Deep Learning course, as I did in 2010 to study differential equations which significantly contributed to my DMA research. For this, I began studying and analyzing Python and Keras programming languages and codes on the Google Colab platform to implement my own Deep Learning model. For about two months, I played with the code and could make the computer learn about 110 piano pieces written by Mozart. Then, after between one and six hours of each learning process (ca. 20-200 epochs in deep learning), the computer wrote a new piano work within its understanding of the music of Mozart. In other words, the computer wrote a pastiche piece in the style of Mozart, or even tried to counterfeit the works by Mozart.

Deep Learning generated Output 020, sequence size 25, temperature 2, 74 epochs of learning

Deep Learning generated Output 062-2, 109 learned works, sequence size 256, weight: 0.085, learning rate: 0.001, optimization: RMSProp, 200 epochs of learning, temperature 3.7

Deep Learning generated Output 063-6, 109 learned works, sequence size 256, weight: 0.085, learning rate: 0.001, optimization: RMSProp, 30 epochs of learning, temperature 3.9, seed piece: Fantasy in c minor KV366

Original handwritten score of On a Winter’s Night a Traveller, The Deeply Learned Clavier
Because of the limit of my access to the Google Colab platform, I couldn’t spend enough time on the deep-learning process of more than six hours for each output, and also the number of model data-works was not enough to generate a real Mozart-like piano work, e.g., having an Alberti bassline or crisp and concise phrase models which we can easily find in his oeuvre. However, those outputs/works generated by the computer implied various interesting features that we can often find in the tonal music repertoires, including ambiguous tonalities (in-between different keys), diatonic scales, repetitions, chords and arpeggios, oftentimes realized in awkward, crude and rudimentary, anti-contrapuntal and artificial, or even distorted and mechanic ways.
For about a month I listened to the outputs generated by the computer, and began tracing the trajectories of the computer’s thoughts. I was almost an archeologist who discovered a pile of unfinished, improvisatory, spurious sketches written by an unknown composer or had been misattributed to Mozart(‘s virtual clumsy pupil, if more accurately described.) During the discovery process, I tried to reveal the computer’s intentions, develop his/her imagination, and transformed it into my own artwork.
This project is currently a work-in-progress. Although I tried to complete it by January 2023, because of my other workload, I hope to finish the piece by the Spring or Summer of 2023. It is commissioned by the Boston-based pianist Ariel Mo, who beautifully world-premiered my Le Tombeau de Harvey in January 2022.
